В период экономического кризиса, в поисках эффективных и рациональных путей его преодоления, экономика Российской Федерации претерпевает существенные изменения. В этой связи управляющие органы регионов страны сталкиваются с проблемами расстановки приоритетов в своей инвестиционной и социально-экономической деятельности. Одной из главных задач при этом остается оценка эффективности инвестиционного развития региона и выработка стратегии ее реализации. Определим количественную оценку эффективности инвестиционной стратегии региона (ИСР) как разность оценки инвестиционного потенциала региона в форме максимизации добавленной стоимости регионального совокупного производителя при использовании имеющегося инвестиционного ресурса, и оценки инвестиционного риска, определяемого численно через финансовые затраты на восстановление работоспособности системы при реализации рисковых случаев. Максимизацию указанного сальдо будем рассматривать как цель разработки инвестиционной стратегии региона.
Из-за сложности региональной социально-экономической системы (СЭС) решить указанные задачи практически невозможно без использования математического моделирования (ММ), разработки автоматизированных информационных систем (АИС) и систем поддержки принятия решений (СППР). Перечисленный комплекс задач также требует внутренней согласованности, ибо не каждая математическая модель может лечь в основу создаваемой СППР, например, в связи с отсутствием эффективных численных алгоритмов ее анализа или требуемой для функционирования АИС информации. Как показано в работах [3–6], к основным требованиям при разработке комплекса «ММ – АИС – СППР» целесообразно отнести следующие:
1) оптимизационность и наличие эффективных алгоритмов анализа математической модели региональной СЭС;
2) сбалансированность входной информации, на основе которой создается АИС;
3) интуитивно понятный для специалистов (инвестиционных аналитиков, управленцев и др.) интерфейс СППР.
Постановка задачи и основная концепция
Пусть инвестиционная стратегия в регионе осуществляется экономическим агентом (ЭА), представляющим собой управляющий орган, заинтересованный в эффективном функционировании региона, как социально-экономической системы «производитель – потребитель». Производитель имеет начальный капитал (собственные или заемные свободные финансовые и материальные средства). У него существует возможность организовать производство n видов продукции (в том числе инновационной), купив или арендовав активные основные производственные фонды (ОПФ) – машины, станки, оборудование, здания, оргтехнику и т.п. Потребитель получает от производителя средства к существованию (заработная плата) и тратит их на свою потребительскую корзину (ПК). Управляющий центр организует взаимодействие ЭА путем взимания налогов и распределения финансового ресурса. При этом функционирование каждого ЭА в социально-экономической системе, в частности региональной, связано с возникновением многочисленных рисков производственного, инвестиционного, финансового, социального и другого характеров. Например, для управляющего центра это может быть необходимость осуществления затрат на поддержку производственных, экологических и социальных программ, для производителя – вложений в очистные сооружения, для потребителя – на поддержание здоровья в связи с нарушением экологических норм и т.п. Кроме того, для всех экономических агентов в СЭС должны отслеживаться риски их неплатежеспособности.
Поставим следующую задачу функционирования региона. Необходимо в региональной СЭС организовать такое взаимодействие экономических агентов, при котором исключается его кризисное экономическое и социальное состояние и развитие. Указанная цель, в частности, может быть достигнута при условии бескризисного развития региональных ЭА.
Для решения задачи определим риск кризисного развития СЭС как «…потери вследствие неправильно поставленной или недостигнутой стратегической цели» [2] при ее функционировании. В качестве стратегических целей ЭА или всей СЭС можно рассматривать максимизацию добавленной стоимости или собственных средств, устойчивое развитие подсистем с выполнением ограничений их функционирования (например, баланса спроса-предложения материальной или финансовой продукции) и т.п. При этом для численной оценки риска, на наш взгляд, целесообразно использовать такой показатель, как уровень затрат (в материальном или стоимостном выражении) на восстановление работоспособности системы при реализации выделенных рисков. Исходя из экспертно определенных данных о рисках по каждому из направлений рискового функционирования региона (производственное, потребительское, коммерческое, финансовое и т.п.), можно построить математическую модель региональной СЭС, с точки зрения минимизации рисков ее кризисного состояния и/или функционирования, путем оценки осуществляемых затрат (как ограниченного сверху финансового ресурса) на избежание (устранение) рисков.
Будем считать результатом решения задачи формирования ИСР такое оптимальное распределение имеющегося объема инвестиционного ресурса по каждому из n видов продукции (отраслей, направлений его экономической деятельности и пр.), производимой в регионе, при котором решается многокритериальная задача максимизации добавленной стоимости региональной СЭС с учетом социальных, экономических и других интересов ЭА.
Для этого предположим, что в региональной СЭС заданы (найдены) зависимости ri = fi(x) рисков ri кризисного развития системы в i-м направлении (i = 1, …, m; m – количество направлений) обеспечения экономической, экологической, финансовой, бизнес- и прочих видов безопасности от вектора затрат х I Rl (l – количество статей затрат) на их избежание (устранение, исключение, уменьшение). Следует отметить, что при математическом моделировании традиционно учитывается часть рисков функционирования СЭС. В частности, к ним относятся риски неплатежеспособности и/или недофинансирования ЭА, недо- и/или перепроизводства продукции.
В работе [6] построена математическая модель региональной СЭС, учитывающая перечисленные риски в случае линейности функций fi (то есть fi = ai – bix). Линейность функций fi в данном случае позволяет строить оптимизационные модели функционирования СЭС и алгоритмы их численного анализа, применимые в практически значимых диапазонах размерностей искомых переменных, что также определяет возможность разработки соответствующих СППР.
Сформулируем далее ряд предпосылок, используемых для упрощения, при моделировании описанной выше задачи.
1. Выполняется принцип «чистых отраслей» (каждый вид продукции в СЭС производится с помощью одного комплекта (вида) ОПФ).
2. Рассматриваются три агрегированных ЭА – управляющий (налоговый) центр, обобщенный производитель и обобщенный потребитель.
3. Все ЭА располагают либо собственными, либо заемными (дотации) средствами для финансирования своей деятельности, а также избежания (устранения) своих рисков.
4. Производимая в СЭС продукция разделяется на 2 типа – потребляемая вне региона и потребляемая внутри региона (входящая в потребительскую корзину).
5. При функционировании СЭС рассматриваются лишь те виды налогов и сборов, которые зависят от искомых объемов инвестиций и производства продукции – налоги на добавленную стоимость (НДС), на имущество (НИ), на прибыль (НП), на доходы физических лиц (НДФЛ), страховые взносы в социальные фонды (СВ) и другие.
6. ОПФ, используемые при производстве любой продукции, функционируют в условиях своей максимальной загрузки (имеют максимальную фондоотдачу).
Математическая модель
Рассмотрим математическую постановку задачи, предварительно сгруппировав все описываемые параметры в три основных блока – производственный, инвестиционно-финансовый и показателей внешней рыночной среды.
Производственный блок:
- n – количество видов продукции;
- n1 – количество видов продукции, не входяших в ПК потребителя;
- ck – стоимость единицы k-го ОПФ (д.е./ед.ОПФ);
- Pk – стоимость единицы k-й продукции (д.е./ед.пр.);
- Tk – срок службы k-го ОПФ (лет);
- Vk – производительность k-го ОПФ (ед.пр/ед.ОПФ);
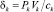 – максимальная фондоотдача k-го ОПФ;
– максимальная фондоотдача k-го ОПФ;- qk – спрос на продукцию k-го вида (д.е./год);
- βk – доли выделяемой на ФОТ выручки от продажи продукции (трудоемкости) производителя k-й продукции;
- θk – стоимость всех видов сырья, использованного на производство продукции (д.е./ед.пр.);
- λk – удельное потребление продукции на одного человека (ед.пр./чел).
- Инвестиционно-финансовый блок:
- α1 ∈ [0; 1] – ставка налога на добавленную стоимость;
- α2 ∈ [0; 1] – ставка налога на имущество;
- α3 ∈ [0; 1] – ставка налога на прибыль ;
- α4 ∈ [0; 1] – ставка страховых взносов в социальные фонды;
- α5 ∈ [0; 1] – ставка налога на доходы физических лиц;
- DS1, DS2, DS3 – соответственно начальные собственные средства производителя, потребителя и управляющего центра (д.е.);
- D1, D2, D3 – соответственно максимальный объем дотаций производителю, потребителю и управляющему центру (д.е.);
- L1, L2, L3 – соответственно максимальные затраты на избежание (устранение) всех выделенных рисков производителя, потребителя и управляющего центра (д.е.);
- Imax – максимальная сумма инвестиций (д.е.).
Внешняя среда:
- T – горизонт планирования (лет);
- r ∈ [0; 1] – номинальная годовая ставка дисконтирования;
- N – численность населения (тыс. чел.).
С учетом приведенных обозначений и предпосылок, а также используя алгоритм расчета прибыли производителя из работы [7], задачу оценки эффективности ИСР можно описать в виде многокритериальной задачи линейного программирования (МЗЛП):
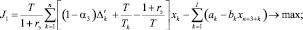 (1)
(1)
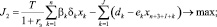 (2)
(2)
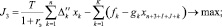 (3)
(3)
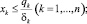 (4)
(4)
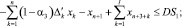 (5)
(5)
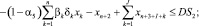 (6)
(6)
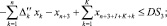 (7)
(7)
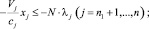 (8)
(8)
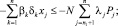 (9)
(9)
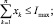 (10)
(10)
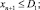
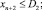
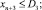 (11)
(11)
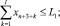
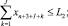
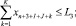 (12)
(12)
xk ≥ 0 (k = 1, ..., n + 3 + I + J + K), (13)
где 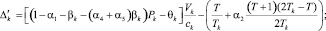
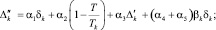 k = 1, …, n;
k = 1, …, n; 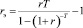 .
.
где I, J, K – соответственно количество рисков для производителя, потребителя и управляющего центра; xk – стоимость приобретаемых ОПФ k-го вида (инвестиции в основные фонды); xn+1, xn+2, xn+3 – дотации производителю, потребителю и управляющему центру соответственно; xn+3+i (i = 1, …, I) – затраты производителя на избежание (устранение) своего i-го риска; xn+3+I+j (j = 1, …, J) – затраты потребителя на избежание (устранение) своего j-го риска; xn+3+I+J+k (k = 1, …, K) – затраты управляющего центра на избежание (устранение) своего k-го риска; rэ – эффективная ставка дисконтирования, учитывающая динамические особенности регионального инвестиционного проекта; ak, dk, fk – максимальные издержки, которые несет ЭА в случае отсутствия затрат на k-ом рисковом направлении своего функционирования; bk, ek, gk – задаваемые экспертно коэффициенты, имеющие смысл для каждого ЭА, оценки значимости эффекта от осуществленных затрат на k-м рисковом направлении своего функционирования; αi, i = 1, …, 6 – соответственно ставки налогов на добавленную стоимость, на имущество, на прибыль, страховых взносов производителя в социальные фонды, подоходного налога потребителя, другой (налоговой и/или неналоговой) затраты производителя.
Cогласно [8], МЗЛП (1)–(13) эквивалентна однокритериальной задаче с теми же ограничениями и максимизацией свертки целевых критериев
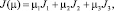
где 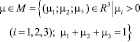 – вектор параметров; R3 – трехмерное евклидово пространство. Многокритериальный анализ описываемой СЭС (поиск Парето-оптимальных инвестиционных стратегий и достижение компромисса интересов экономических агентов) – регионального управляющего (налогового) органа, обобщенного производителя и обобщенного потребителя в регионе – можно осуществлять с помощью системы поддержки принятия решений, описанной в работе [1]. Для обеспечения разрешимости модели (1)–(13), при всех значениях входящих в нее параметров, неравенства (8) и (9) могут быть исключены из модели, а описываемые ими условия учтены путем параллельного переноса Парето-множества задачи вдоль критериальной оси J2 потребителя.
– вектор параметров; R3 – трехмерное евклидово пространство. Многокритериальный анализ описываемой СЭС (поиск Парето-оптимальных инвестиционных стратегий и достижение компромисса интересов экономических агентов) – регионального управляющего (налогового) органа, обобщенного производителя и обобщенного потребителя в регионе – можно осуществлять с помощью системы поддержки принятия решений, описанной в работе [1]. Для обеспечения разрешимости модели (1)–(13), при всех значениях входящих в нее параметров, неравенства (8) и (9) могут быть исключены из модели, а описываемые ими условия учтены путем параллельного переноса Парето-множества задачи вдоль критериальной оси J2 потребителя.
Таким образом, в данной работе представлена математическая модель оценки эффективности инвестиционной стратегии региона. Проведенные с помощью пакета [1] предварительные численные расчеты, на модельных данных для ряда частных случаев модели, показали существование нетривиального решения в ней.
Библиографическая ссылка
Медведев А.В., Ощепкова Н.С., Победаш П.Н., Трусов А.Н. РАЗРАБОТКА МАТЕМАТИЧЕСКОЙ МОДЕЛИ ОЦЕНКИ ЭФФЕКТИВНОСТИ ИНВЕСТИЦИОННОЙ СТРАТЕГИИ РЕГИОНА // Фундаментальные исследования. – 2016. – № 10-1. – С. 62-66;URL: https://fundamental-research.ru/ru/article/view?id=40809 (дата обращения: 18.04.2024).



