Научный журнал

Фундаментальные исследования

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Абрегов М.Х. 1 Канчукоев В.З. 1 Машуков И.К. 1

---

1 ФГБОУ ВПО «Кабардино-Балкарский государственный университет им. Х.М. Бербекова»

Работа посвящена построению устойчивого численного метода решения задачи Коши для линейного обыкновенного дифференциального уравнения второго порядка, которая часто используется при исследовании прикладных задач физики, техники, биологии и других областей науки. Известно, что решение данной задачи может оказаться неустойчивым. В таком случае сложно получить ее решение численно, поскольку ошибки округления и усечения оказывают на результат такое же влияние, как и изменение начальных условий. Предложенный в работе метод основывается на редукции исходной задачи Коши к эквивалентной задаче для линейного обыкновенного дифференциального уравнения второго порядка с нелокальным интегральным условием и последующем ее решении конечно-разностным методом. Конечно-разностная схема, аппроксимирующая дифференциальную задачу с нелокальным условием со вторым порядком точности по шагу сетки, сводится к решению двух устойчивых конечно-разностных схем второго порядка с граничными условиями первого рода.

Статья в формате PDF

1026 KB

задача коши для обыкновенного линейного дифференциального уравнения второго порядка

устойчивость решения

численный метод решения

априорная оценка

1. Бахвалов Н.С., Жидков Н.П., Кобельков Г.М.. Численные методы. – М.: Наука, 1987.

2. Ортега Дж., Пул У.. Введение в численные методы решения дифференциальных уравнений. – М.: Наука, 1986.

3. Самарский А.А.. Теория разностных схем. – М.: Наука, 1989.

4. Самарский А.А., Гулин А.В. Численные методы. – М.: Наука, 1989.

5. Степанов В.В. Курс дифференциальных уравнений. – М.: Государственное издательство технико-теоретической литературы, 1956.

Рассмотрим задачу Коши для линейного дифференциального уравнения второго порядка

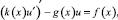0 < x < l; (1)

u(0) = 0; 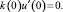(2)

Будем предполагать, что коэффициенты и правая часть уравнения (1) удовлетворяют условиям: k(x) ∈ C3[0, l]; g(x), f(x) ∈ C2[0, l]; c2 ≥ k(x) ≥ c1 > 0; .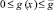

Известно [5], что решение задачи (1)–(2) существует и единственно в классе функций C4[0, l]. Однако это решение, как показано в [2], при больших значениях l может оказаться неустойчивым. Это означает, что сколь угодно малые изменения начальных условий могут вызвать сколь угодно большие изменения решения при больших значениях l. В этом случае сложно получить указанное решение численно, так как ошибки округления и усечения оказывают такое же влияние, как и изменение начальных условий, и приводят к тому, что решение становится неограниченным.

Проинтегрировав уравнение (1) по отрезку [0, l] и воспользовавшись начальным условием (2), приходим к эквивалентной задаче

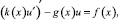x ∈(0, l); (3)

u(0) = 0; (4)

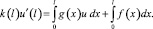(5)

На равномерной сетке

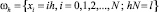
задачу (3)–(5) аппроксимируем конечно-разностной схемой

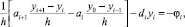
i = 1, 2, ..., N – 1;

y0 = 0; (6)

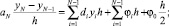
где

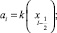di = g(xi); φi = f(xi). (7)

Нетрудно показать, что разностная схема (6) аппроксимирует дифференциальную задачу (3)–(5) с точностью 0(h2). Используя обозначения [3]

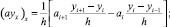
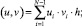
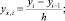
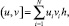
перепишем задачу (6) в форме

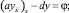(8)

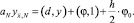y0 = 0; (9)

Нетрудно показать единственность решения задачи (8), (9). Действительно, есл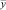и и – два решения задачи (8), (9), то, очевидно, разность 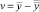будет решением задачи

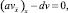i = 1, 2, ..., N – 1, (10)

v0 = 0; 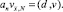(11)

Суммируя (10) по i от 1 до N – 1, приходим к равенству

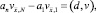
из которого следует, с учетом условия (22), что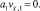

Таким образом, сеточная функция v будет решением конечно-разностной задачи Коши

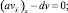v0 = 0;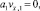

из которой следует, что vi = 0, i = 0, 1, ..., N, что означает единственность решения задачи (8), (9).

Будем искать решение задачи (8), (9) в виде

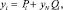i = 0, 1, ..., N, (12)

где Pi и Qi – сеточные функции, определенные на сетке ωh, как решения разностных задач:

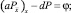P0 = 0; PN = 0; (13)

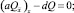Q0 = 0; QN = 1, (14)

где коэффициенты a, d и правая часть φ определены по формулам (7). Как известно [3], задачи (13) и (14) однозначно разрешимы в силу условий на a, d.

Для решения задачи (13) имеет место априорная оценка [4]

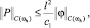(15)

а для решения задачи (14) имеет место равномерная оценка

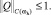(16)

Непосредственной подстановкой можно убедиться, что функция y, определенная по формуле (12), удовлетворяет уравнению (8) и начальному условию y0 = 0. Подставив (12) в нелокальное условие (9), приходим к равенству

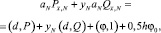
откуда выражаем yN:

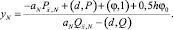(17)

Покажем ограниченность yN. Преобразуем правую часть (17). Суммируя уравнение (13) по i от 1 до N – 1, приходим к равенству

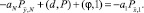(18)

Суммируя уравнение (14) по i от 1 до N – 1, получаем

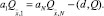(19)

С учетом (18) и (19) выражение (17) для yN принимает вид

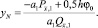(20)

Оценим снизу 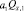. Это число не может быть отрицательным, что противоречило бы принципу максимума [3] первой краевой задачи для уравнения (14). Также 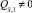, это противоречит условию QN = 1. Следовательно, .

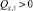Пусть ri – сеточная функция, определенная на ωh, и является решением разностной задачи

r0 = 1; rN = 0. (21)

Умножим уравнение (21) скалярно на Q, а уравнение (14) скалярно на r и вычтем почленно одно из другого. Применяя разностную формулу интегрирования по частям [3] и учитывая краевые условия (14), (21), приходим к равенству

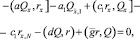
откуда находим

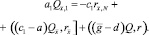(22)

Нетрудно показать, что для всех i = 1, 2, ..., N выполняются неравенства

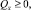
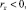Q ≥ 0, r ≥ 0.

С учетом этих оценок из (22) получаем

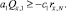(23)

Оценим снизу выражение 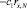. Используя точное решение задачи (21), находим, что

,

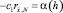где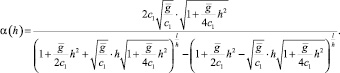

Положив

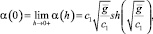
на отрезке 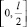получим непрерывную, возрастающую по h функцию. Следовательно, для любого 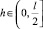имеет место неравенство 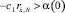. Таким образом, 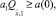откуда следует, что

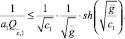(24)

Теперь оценим сверху модуль выражения 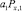. Умножая скалярно разностное уравнение (13) на сеточную функцию 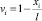, определенную на ωh, получим

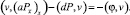(25)

Применяя разностную формулу интегрирования по частям [4] в (25) и учитывая краевые условия (13) и равенства 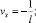vN = 0, v0 = 1, получаем

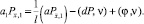(26)

Применяя неравенство Коши – Буняковского [1, 3], оценим по модулю слагаемые в правой части (26):

а)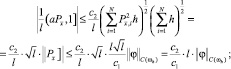

б)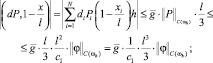

в)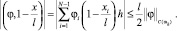

С учетом полученных оценок и неравенства 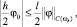из (26) находим

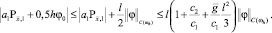(27)

Из (24) и (27) получаем оценку

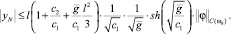(28)

Из (12), используя оценки (15), (16) и (28), получаем равномерную оценку решения конечно-разностной схемы (8), (9),

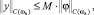(29)

где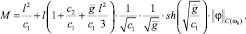

Из оценки (29) следует устойчивость конечно-разностной схемы (8), (9). Алгоритм решения задачи (8), (9) заключается в решении задач (13) и (14) методом прогонки [3], вычислении yN по формуле (20) и подстановке их в формулу (12). В силу условий на коэффициенты в задачах (13) и (14) метод прогонки при их решении будет устойчивым, погрешность в исходных данных не будет возрастать.

Изложенный выше метод можно использовать для нахождения решения задачи (1), (2) с более высоким порядком точности по шагу h.

Библиографическая ссылка