ФУНКЦИОНАЛЬНЫЕ СВЯЗИ В КОМПЛЕКСИРОВАННЫХ ИСПОЛНИТЕЛЬНЫХ СИСТЕМАХ ТЕХНОЛОГИЧЕСКИХ РОБОТОВ И ИХ НАРУШЕНИЯ
1
Умнов В.П.
1
Егоров И.Н.
1
1 ФГБОУ ВПО «Владимирский государственный университет имени Александра Григорьевича и Николая Григорьевича Столетовых»
Новым направлением в создании оборудования для изготовления деталей сложной формы являются машинные центры гибридной обработки, включая аддитивные технологии. Функциональные возможности таких центров позволяют изготавливать новые детали до уровня готовой продукции, а также осуществлять их ремонт и доработку, например, упрочнение поверхности. Сформулирована задача создания высокоэффективных робототехнических комплексов для автономной работы при выполнении гибридных операций в гибком производстве. Такие комплексы должны обладать многофункциональной манипуляционной исполнительной системой, обеспечивающей необходимые параметры управляемого движения и взаимодействия рабочих инструментов. Приведен пример такой системы и показаны функциональные связи, существующие в ней. Предложена классификация возможных нарушений связей, включая сингулярности. Предложена методика итерационного синтеза кинематической цепи манипуляторов, исключающая сингулярности, а также отмечены направления устранения нарушений функциональных связей.
гибридная обработка
манипуляционная система
функциональные связи
нарушения связей
синтез
1. Власенков, А.В. Геометрический синтез кинематической структуры манипуляционных систем технологических роботов и роботов-станков / А.В. Власенков, В.П. Умнов, А.А. Петров // Проблемы машиностроения и автоматизации. – 2011. – № 2. – С. 123–125.
2. Глазунов В.А. Cтруктура пространственных механизмов. Группы винтов и структурные группы // Инженерный журнал. Справочник. – 2010. – № 3. – С. 1–24.
3. Крайнев А.Ф. Новые механизмы относительного манипулирования / А.Ф. Крайнев, В.А. Глазунов // Проблемы машиностроения и надежности машин. – 1994. – № 5. – С. 106–117.
4. Умнов, В.П. Комплексирование манипуляционной исполнительной системы роботизированных технологических центров гибридной обработки / В.П. Умнов, И.Н. Егоров, С.В. Молостов // Современные проблемы науки и образования. – 2014. – № 1.
5. Патент 2482945 Российская Федерация. МПК В23К 26/08 Устройство для лазерной обработки / Умнов В.П., Егоров И.Н., Гольцова Е.А. и др. – № 2012115334/02 заявл.16.04.2012; опубл. 27.05.2013, бюл. № 15].
6. DMG / MORI SEIKI SYSTEMS – DMG MORI – PDF Catalogue. URL: http: // pdf directindystri. com / pdf / dmg-mori-systems / 5973-52069. html. (дата обращения 18.11.15).
Технологией нового поколения является гибридная обработка, реализуемая в машинных центрах. Характерным представителем этого направления является обрабатывающий центр компании «DMG MORI» LASERTEC 65 3D [6], осуществляющий обработку резанием в сочетании с лазерной наплавкой с качеством готовой детали для производства, ремонта и нанесения покрытий.
В последние годы целый ряд основных операций в механической обработке стали успешно выполнять промышленные роботы (фрезерование концевыми фрезами, шлифование, полирование и другие) с погрешностью обработки до 0,01 мм. Преимущества использования роботов следующие: стоимость робота в несколько раз меньше стоимости 5-координатного станка с ЧПУ; высокая маневренность (в одной роботизированной ячейке можно организовать несколько рабочих зон); гибкость функционирования (вариативность решений «инструмент к детали», «деталь к инструменту» или совместные движения инструмента и детали в процессе выполнения операции); значительно меньшая масса и потребление энергии в процессе работы. Роботы являются одним из основных рабочих инструментов при обработке концентрированными потоками энергии, доминирующей из которых является лазерная. Исходя из сказанного, можно считать, что создание высокоэффективных комплексированных робототехнических центров для выполнения гибридных операций на основе принципов мехатроники является важной и актуальной задачей. Подобный центр должен обладать специализированной многофункциональной манипуляционной исполнительной системой, обеспечивающей необходимые параметры управляемого движения и взаимодействия рабочих инструментов.
В качестве примера на рис. 1 представлен вариант построения манипуляционной системы роботизированного центра гибридной обработки для восстановительного ремонта рабочей поверхности турбинных лопаток.
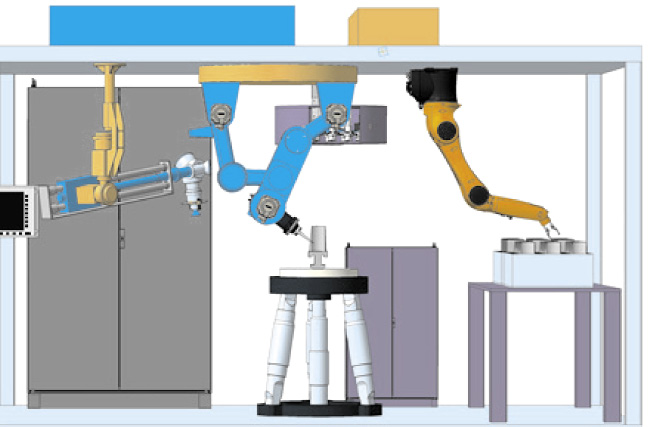
Рис. 1. Вариант построения манипуляционной системы роботизированного центра гибридной обработки
Здесь обозначено: 1 – основной технологический манипулятор (ОТМ) с исполнительным механизмом параллельной структуры; 2 – трипод с поворотным столом, на котором устанавливается обрабатываемая деталь (МРИ) – 7; 3 – дополнительный транспортный манипулятор (ДТМ) для загрузки рабочей позиции; 4 – пассивный манипулятор (МО), необходимый для выполнения лазерной операции (специализированный инструмент для транспортировки лазерного излучения, подачи наплавочного материала и технологических газов); 5 – магазин заготовок и готовых изделий (МЗ); 6 – магазин инструментов (МИ).
Манипуляционная система роботизированного центра гибридной обработки, представленная на рис. 1, является многомерным объектом управления и регулирования позиционными кинематическими, силовыми, энергетическими и температурными параметрами. Управление подобным объектом, по сути, является управлением имеющимися функциональными связями и проявляющимися взаимодействиями. Во время движения позиционная связь и силовое взаимодействие неразрывно связаны, являясь, по сути, позиционно-силовым взаимодействием на втором уровне постоянно, а на первом – в зависимости от положения компонентов системы и выполняемой операции. На рис. 2 приведена структурная схема связей и взаимодействий в рассматриваемой манипуляционной системе, которую в определенной степени можно принять в качестве обобщенной [4].
Операции, выполняемые манипуляционной системой, осуществляются в условиях параметрической и структурной неста ционарности состояния позиционных кинематических и оптических связей, а также силовых взаимодействий между рабочим органом и объектом работ, отдельными манипуляторами и их звеньями. В манипуляционной системе могут возникнуть непреднамеренные нарушения имеющихся функциональных связей, приводящие к их неопределенности или несоответствию заданным параметрами, обуславливающие невозможность роботу выполнять свои действия в процессе работы. То есть реализация текущего фазового перехода станет невозможной. При этом предполагается, что отмеченные нарушения не являются следствием сбоя или выхода из строя какого-либо компонента робототехнической системы. В робототехнике подобными нарушениями считаются особые положения механизмов исполнительных кинематических цепей, в которых решение обратной задачи кинематики становится неопределенным. Пристальное внимание особым положениям уделяется при рассмотрении механизмов параллельной структуры, в которых может теряться их подвижность или управляемость [2, 3].
Устранение сингулярностей в роботах с механизмами параллельной структуры осуществляется путем соответствующего проектирования раздельных механизмов (зон работы небольших размеров), использованием избыточности или дополнительных приводов или построением траектории, при движении по которой робот может преодолеть возможные особые положения. В последнем случае используется параллельная динамическая модель исполнительной системы и метод вычисления управляющих моментов.
На основании приведенных выше общих рассуждений, опыта моделирования и анализа работ на рис. 3 представлен вариант классификации нарушений функциональных связей в манипуляционных исполнительных системах роботов.
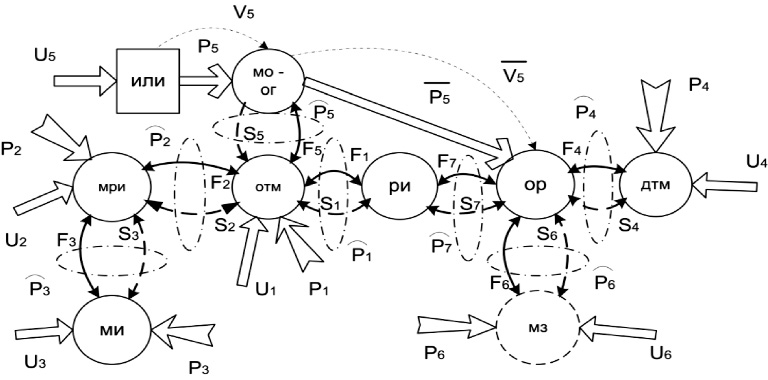
Рис. 2. Входные воздействия, связи и взаимодействия в обобщенной манипуляционной системе: Ui, i = 1,6 – управляющие воздействия; Sj,j = 1,7 – стационарная или нестационарная направленная позиционная кинематическая связь; Fk, k = 1,7 – стационарное или нестационарное направленное силовое воздействие; Pl, l = 1,6 – мощность, подводимая к компонентам манипуляционной системы; P5 – мощность лазерного излучения, воздействующего на объект работ; Pm, m = 1,7 – мощность, передаваемая во время движения в результате позиционно-силового взаимодействия; V5 и 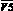 позиционная оптическая взаимосвязь, характеризующая пространственное положение лазерного луча
позиционная оптическая взаимосвязь, характеризующая пространственное положение лазерного луча
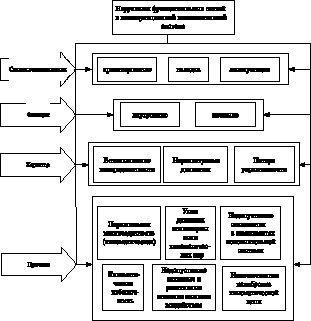
Рис. 3. Классификация нарушений в исполнительных системах манипуляционных роботов
На стадии проектирования наличие особых положений (возможность потери подвижности и (или) управляемости) в исполнительной кинематической цепи чаще всего определяется в процессе решения обратных задач поиском вырожденных якобианов. Для исключения этих положений ищется соотношение размеров звеньев, которое может оказаться не оптимальным
Предлагается методика, построенная на использовании прямых и обратных дифференциальных преобразований над множеством допустимых конфигураций исполнительной кинематической цепи манипуляционной системы {GK}, 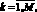 таких, что
таких, что 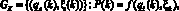
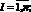 i ? gk. Необходимо определить конфигурацию Gc = f(qnc, ?c), при которой во время движения характерной точки p с постоянной контурной скоростью
i ? gk. Необходимо определить конфигурацию Gc = f(qnc, ?c), при которой во время движения характерной точки p с постоянной контурной скоростью 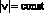 ускорения в обобщенных координатах
ускорения в обобщенных координатах 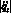 были минимальными или не превышали некоторых допустимых значений [1]. В обозначениях gk – множество индексов i, допустимых конфигурацией gn(k), ?(k) для k-й узловой точки; x(k) – конструктивный параметр, отражающий геометрические размеры звеньев. При этом исключаются особые положения и осуществляется оптимизация по следующему алгоритму:
были минимальными или не превышали некоторых допустимых значений [1]. В обозначениях gk – множество индексов i, допустимых конфигурацией gn(k), ?(k) для k-й узловой точки; x(k) – конструктивный параметр, отражающий геометрические размеры звеньев. При этом исключаются особые положения и осуществляется оптимизация по следующему алгоритму:
1. По граничным точкам рабочей зоны определяется предварительная базовая конфигурация исполнительной кинематической цепи {G?}, характеризующаяся диапазоном изменения обобщенных координат qi? и конструктивным параметром ??. При этом должно выполняться условие ?qi? ? [qi].
2. Для граничной точки траектории k = 1 решается обратная задача о положении точек и звеньев манипуляционной системы по выражению
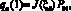 (1)
(1)
где J(??) – функциональная матрица обратного преобразования, P01 = [X01, Y01, Z01, ?01, ?01, ?01] – линейные координаты и угловое положение рабочего инструмента в базовой системе координат.
3. По заданной контурной скорости Р определяются скорости обобщенных координат, используя выражение:
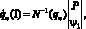 (2)
(2)
где N–1 – инвертированный якобиан; y – угловая скорость движения инструмента, определенная с учетом его заданного числового положения к траектории движения в точке (для k = 1 можно принять 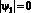 ).
).
4. Считая, что qn = qn(f), по выражениям (1) и (2) определяются значения q(2) и 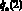 для точки k = 2. Поскольку
для точки k = 2. Поскольку 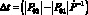 , то
, то 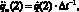 где
где 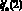 – ускорения обобщенных координат в точке Р2.
– ускорения обобщенных координат в точке Р2.
5. Оцениваются величины ускорений для каждой обобщенной координаты. Если 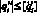 , то переходим к следующей точке траекторий. Если для некоторой j-й координаты это условие не выполняется, то необходимо выполнить коррекцию конфигурации {G?}. Для этого в выражении
, то переходим к следующей точке траекторий. Если для некоторой j-й координаты это условие не выполняется, то необходимо выполнить коррекцию конфигурации {G?}. Для этого в выражении 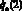 определяется наибольшая составляющая обобщенной скорости
определяется наибольшая составляющая обобщенной скорости 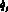 и, меняя постоянные коэффициенты в этой составляющей, методом последовательных приближений получаем условие
и, меняя постоянные коэффициенты в этой составляющей, методом последовательных приближений получаем условие 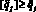 .
.
6. Выполняется процедура определения конфигураций для всего множества {Pk}, k = 1, M положений рабочей точки на кривой l. В результате получается М конфигураций, из которых, при решении задачи по допустимому ограничению ускорения обобщенных координат, ряд конфигураций могут повторяться и быть объединены в соответствующие подмножества.
7. Производится анализ полученных конфигураций. При этом для параметров x(k), которые в процессе формирования конфигураций {Gk}, k = 1, M изменялись, может использоваться математическое ожидание их величин. Получаем синтезированную конфигурацию {Gc}.
8. Выполняется контрольная проверка {Gc} для точек траектории на соответствие всем условиям решения задачи синтеза. При соответствии условиям решение задачи заканчивается. При несоответствии следует продолжить решение, начиная с п. 3 до получения окончательного результата. Если решение не сходится, следует изменить условие задачи, в частности допустимые ограничения [qi].
Для построения алгоритмов управления и создания управляющих программ, в том числе с использованием виртуальных симуляторов, необходима параметрическая идентичность исполнительной системы и ее модели. Выполнение идентификации по сборочным чертежам затруднительно, поскольку детали изготавливаются с допусками на размеры и совокупный размер в собранном узле может быть достаточно точно определен только эмпирически. При значительном несоответствии параметров модели и реального объекта, например длин звеньев исполнительной кинематической цепи, может нарушиться функциональная связь между управляющей программой и необходимой траекторией движения рабочего органа, и операции с наложенными связями могут стать невыполнимыми. Исходя из этого, необходима качественная параметрическая идентификация (калибровка) исполнительной системы с использованием современного метрологического обеспечения.
Под потерей управляемости в робототехнике понимается возможность самопроизвольного перемещения выходного звена в исполнительных механизмах параллельной структуры при отсутствии управляющих моментов за счет их кинематических особенностей. В классическом понимании потерей управляемости является невозможность перевода системы из начального состояния в конечное при помощи некоторого входного сигнала, то есть невозможность реализации фазового перехода.
Частным случаем такой потери управляемости является недопустимое смещение оси луча в зеркальной оптической системе СО2 лазер – робота. Процесс управления положением лазерного луча и точки фокуса в пространстве, являющейся, по сути, основным процессом, осуществляется опосредованно в функции состояния исполнительной системы манипулятора оптики и внешних воздействий на него.
Потеря управляемости может быть вызвана упругими деформациями звеньев исполнительной кинематической цепи. Для исключения этого явления может быть использовано устройство управления, предложенное в [5].
Работа выполнена при финансовой поддержке РФФИ (проект № 13-08-01364).
Библиографическая ссылка
Умнов В.П., Егоров И.Н. ФУНКЦИОНАЛЬНЫЕ СВЯЗИ В КОМПЛЕКСИРОВАННЫХ ИСПОЛНИТЕЛЬНЫХ СИСТЕМАХ ТЕХНОЛОГИЧЕСКИХ РОБОТОВ И ИХ НАРУШЕНИЯ // Фундаментальные исследования. – 2015. – № 12-5.
– С. 955-959;
URL: https://fundamental-research.ru/ru/article/view?id=39658 (дата обращения: 25.04.2024).
Предлагаем вашему вниманию журналы, издающиеся в издательстве «Академия Естествознания»
(Высокий импакт-фактор РИНЦ, тематика журналов охватывает все научные направления)






