Основным инструментом описания процесса распространения оптического излучения через сильно рассеивающие среды (СРС), такие как биологические ткани, является уравнение переноса излучения (УПИ). Оно представляет собой интегро-дифференциальное уравнение баланса энергии в среде, содержащей частицы [7]. Главная проблема заключается в том, что УПИ в общем виде не имеет аналитического решения, так как рассеяние фотонов является случайным. По этой причине для описания распространения оптического излучения в СРС с коэффициентами поглощения и рассеяния в ближнем инфракрасном диапазоне как у биологических тканей используются различные приближённые модели [1?4]. Чаще всего используются многопотоковые модели (метод Кубелки ? Мунка), моделирование методом статистических испытаний (Монте-Карло) и диффузионное приближение к УПИ.
Главным допущением метода Кубелки ?Мунка является то, что лучевая интенсивность считается диффузной. Внутри ткани (при одномерной геометрии) поток фотонов разделяется на два: в направлении падающего излучения и в обратном направлении (рассеяние назад). Лучевая интенсивность в каждом направлении испытывает два акта снижения (из-за поглощения и рассеяния) и один акт усиления (из-за рассеяния фотонов с противоположного направления). Основным недостатком метода является адекватность только в случаях, когда рассеяние многократно превышает поглощение [2, 10].
Главным допущением метода Монте-Карло является то, что макроскопические оптические свойства считаются одинаковыми в пределах небольших объемов ткани. Метод заключается в статистическом моделировании случайного движения большого числа фотонов внутри биологической ткани с учетом актов поглощения и рассеяния на всем оптическом пути каждого из них [10]. Для метода характерна высокая точность и универсальность, но он очень требователен к вычислительной мощности.
Главным допущением диффузионного приближения является то, что ключевым фактором ослабления света признаётся процесс рассеяния (диффузии фотонов). УПИ упрощается посредством разложения в ряд сферических гармоник. Результатом упрощения является система связанных дифференциальных уравнений в частных производных, которая может быть сведена к одному дифференциальному уравнению. Основным достоинством диффузионного приближения является то, что оно хорошо описывает распространение излучения в толще биологической ткани, а недостатком – то, что оно справедливо не во всех случаях, а лишь при больших альбедо и небольших значениях фактора анизотропии рассеяния [8].
Целью данной работы является усовершенствование модели диффузионной миграции фотонов в случайно-неоднородных СРС до уровня, позволяющего моделировать миграцию нормированного максимума фотонной плотности (НМФП) в СРС с оптическими свойствами и структурой биологических тканей.
Материалы и методы исследования
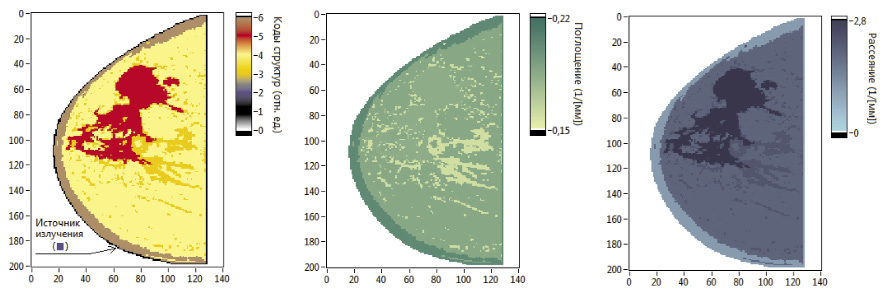
Для численного моделирования оптических свойств биологических тканей разработана универсальная компьютерная модель рецепторного типа. В ней биологические ткани (с геометрической точки зрения) представлены как трехмерные конечные объекты заданной формы, получаемые путем аппроксимации исследуемого биомедицинского объекта конечно-разностной схемой. В качестве источника информации о строении конкретного биомедицинского объекта используются результаты его КТ или МРТ исследования. Для выделения структур биообъекта посредством уменьшения уровней квантовая исходных изображений проводится изогелия (постеризация) всех томограмм. В результате этой операции общее количество полутонов на томограммах сокращается до необходимого пользователю уровня (как правило, до нескольких десятков). Оставшиеся после изогелии полутона кодируются и ставятся в соответствие характерным для исследуемой биологической ткани структурам. Вручную указывается позиция источника излучения. Каждой структуре присваиваются табличные значения коэффициентов поглощения и рассеяния. Таким образом, на основе результатов КТ или МРТ исследования формируется геометрическая модель исследуемого объекта и пространственные распределения коэффициентов поглощения и рассеяния в нём.
Для моделирования миграции фотонов в исследуемом объекте используется диффузионное приближение к УПИ следующего вида [2, 6]:
где ![]() – скорость света в среде; c0 – ско рость света в вакууме; ?object – относительный коэффициент преломления моделируемого объекта (?) и его границы (??); x, y, z – координаты всех точек конечной моделируемой области;
– скорость света в среде; c0 – ско рость света в вакууме; ?object – относительный коэффициент преломления моделируемого объекта (?) и его границы (??); x, y, z – координаты всех точек конечной моделируемой области; ![]() и ?a(x, y, z) – коэффициент диффузии и коэффициент поглощения в точках с координатами x, y, z; ?s(x, y, z) – коэффициент рассеяния в точках с координатами x, y, z; g – параметр анизотропии; ?(x, y, z, t) – фотонная плотность в точке с координатами x, y, z в момент времени t;
и ?a(x, y, z) – коэффициент диффузии и коэффициент поглощения в точках с координатами x, y, z; ?s(x, y, z) – коэффициент рассеяния в точках с координатами x, y, z; g – параметр анизотропии; ?(x, y, z, t) – фотонная плотность в точке с координатами x, y, z в момент времени t; ![]() – функция источника фотонов; ? – дельта-функция,
– функция источника фотонов; ? – дельта-функция, ![]() – средняя длина рассеяния, т.е. глубина на которой возникает точечный виртуальный изотропный источник.
– средняя длина рассеяния, т.е. глубина на которой возникает точечный виртуальный изотропный источник.
Для описания распространения фотонов на границе [8] моделируемого объекта ? используется граничное условие третьего типа (Робина):
![]()
![]()
![]() (2)
(2)
где n(x, y, z) – направление внешней нормали к границе ?? в точке с координатами x, y, z. F – коэффициент френелевского отражения [2], вычисляемый как
![]()
где R0 и Qc – коэффициенты, соответственно равные
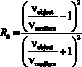 и
и ![]()
где ?medium – относительный коэффициент преломления для окружающей объект среды.
Численное решение уравнения (1) с граничным условием (2) было выполнено по семиточечному шаблону. Начальное приближение функции ?(x, y, z, t) во всех узлах сетки генерируется с учетом геометрии объекта, позиции источника фотонов и количества инжектируемых в исследуемый объект в течение одиночного импульса фотонов. Количество фотонов рассчитывается на основе средней мощности используемого фемтосекундного импульсного лазера, а также его длины волны и длительности одиночного импульса. Критерием окончания итерационного процесса служит истечение заданного времени.
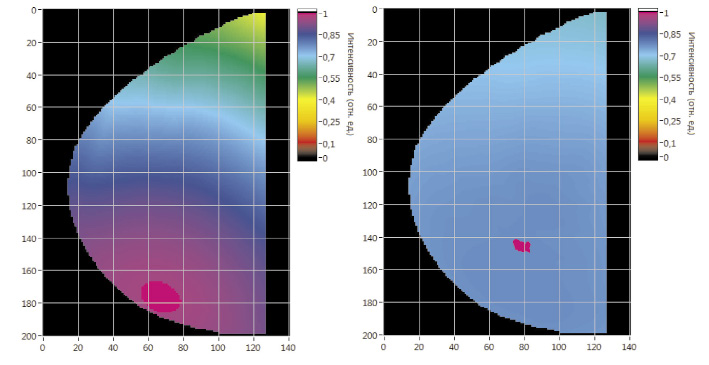
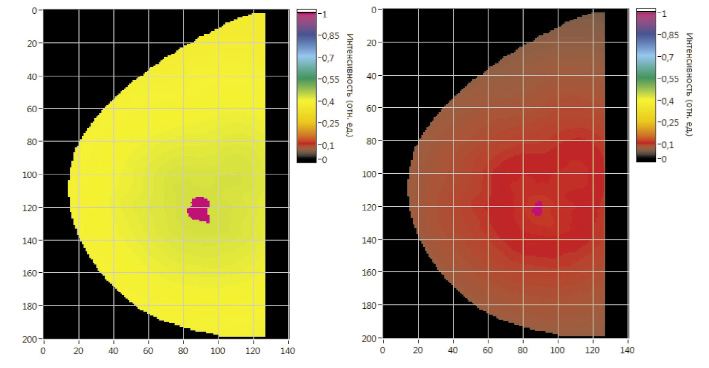
После завершения итерационного процесса для получения НМФП функция ?(x, y, z, t) нормируется [9] относительно своего максимума ?max(x, y, z, t):
![]()
и подвергается следующему преобразованию [9]:
![]()
где P – экспериментально найденный минимальный уровень фотонной плотности НМПФ, 0 < P ? 1.
Результаты исследования и их обсуждение
Вышеописанные модели были практически реализованы в виде специализированных программных продуктов c помощью среды разработки и платформы для выполнения полученных программ LabVIEW.
В качестве биологического объекта для проведения компьютерных экспериментов был выбран маммографический объект [5]. В результате анализа томограмм у исследуемого биообъекта были выделены следующие основные структуры: кожные покровы, жировая ткань, карцинома протока, фиброзно-кистозная и железистая ткани. По этим структурам на основе справочной информации [10] были сформированы геометрическая модель исследуемого объекта (рис. 1, а) и пространственные распределения коэффициентов поглощения (рис. 1, б) и рассеяния (рис. 1, в) в нём.