В составе многих современных систем автоматизации производства часто применяются магнитострикционные преобразователи (МП) различных физических величин, таких как уровень, угол наклона, плотность контролируемого объекта. Это объясняется тем, что МП, обладая низкой себестоимостью, обеспечивают высокую точность, быстродействие и разрешающую способность преобразования.
Разработкой МП занимаются различные отечественные и зарубежные компании, однако российские образцы пока во многом уступают импортным аналогам. Поэтому возникает необходимость проведения исследований подобных приборов с целью повышения эффективности их функционирования. Для этого наиболее привлекательным представляется использование методов математического моделирования магнитных полей и выходных параметров МП. Математическое моделирование МП было выполнено в работах многих авторов, например [1, 3], и это в конечном итоге позволяло добиться оптимальной конструкции приборов.
Основными недостатками известных математических моделей МП являются значительная погрешность при аппроксимации и невысокая скорость сходимости используемых численных методов. Поэтому при моделировании МП со сложной геометрией расчетной области существующими методами не может быть достигнуто высокой точности результата.
В данной статье будет описан способ, позволяющий снизить погрешность при моделировании МП, а также повысить скорость расчета путем снижения числа необходимых итераций.
Постановка задачи
Рассмотрим в качестве примера байпасный магнитострикционный преобразователь уровня (МПУ) накладного типа, расчетная схема которого изображена на рис. 1.
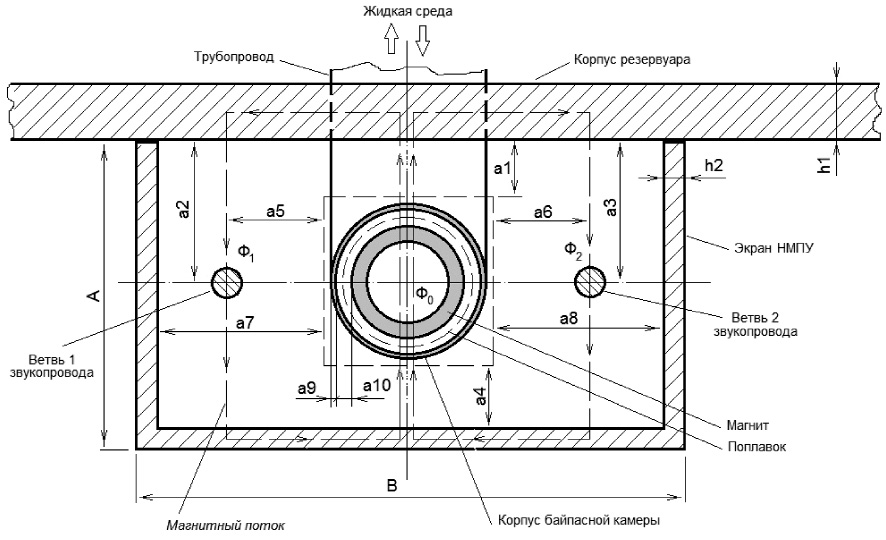
Рис. 1. Расчетная схема байпасного МПУ накладного типа
Математическая модель этого МПУ известна [3, 4], но при этом обладает отмеченными выше недостатками. Это подтверждается проведенными вычислительными экспериментами с использованием разработанного авторами программного комплекса «Моделирование МПУ» [4]. Поэтому возникает задача повышения точности и скорости расчета параметров МПУ путем модификации имеющихся численных методов и комплекса программ.
Методы испытаний
В известной математической модели байпасных МПУ накладного типа [3] переход к разностным уравнениям осуществлялся методом баланса с введением регулярной сетки на расчетной области, а для решения их системы применялась попеременно треугольная итерационная методика.
С целью повышения точности аппроксимации предлагается осуществлять указанный переход на основе интегрального тождества, которое, как известно [2], позволяет решать задачу в общем случае с внесением минимальной погрешности.
При расчете магнитного поля в двумерной расчетной области с заданными краевыми условиями первого рода, интегральное тождество принимает вид [2]:
(1)
где ?, ? – магнитная проницаемость и плотность тока в ячейке; S – её площадь; u – обобщенный скалярный магнитный потенциал; ? – некоторая функция с непрерывной первой и второй производной.
Далее представим интегралы в (1) суммами интегралов по всем ячейкам сетки:
(2)
где M – число ячеек сетки; Sn – площадь n-й ячейки.
Тогда, с учетом разностных соотношений
(3)
где i – номер строки; j – номер столбца сетки, для узла 0 можно записать (рис. 2):
(4)
Стоящие в скобках выражения не зависят от Sn, поэтому могут быть вынесены за знак интеграла. Оставшиеся же интегралы вида 
приближенно заменяются средними значениями магнитной проницаемости ?n = const в каждой ячейке.
После раскрытия всех скобок в левой части (4) коэффициент при ?0 приравнивается к нулю и получается разностное уравнение для узла 0 вида
(5)
где 
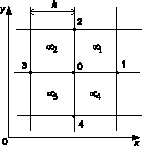
Рис. 2. Схема получения разностных уравнений для узла 0
Такие уравнения могут быть получены для всех узлов сетки расчетной области МПУ накладного типа, кроме тех, что лежат на границе, так как поведение магнитного поля в таких точках известно и определяется граничными условиями. В результате получим систему алгебраических уравнений общим числом N?M, где N, M – количество узлов сетки по вертикали и горизонтали. Решением этой системы будут значения модуля обобщенного скалярного магнитного потенциала u в каждом узле сетки. Искомые значения напряженности 
определим по этим данным на основании определения скалярного магнитного потенциала u [5].
В результате расчет магнитного поля МПУ сводится к решению системы линейных алгебраических уравнений вида
Au = b, (6)
где 
– матрица коэффициентов системы; u – столбец неизвестных (потенциалов); b – столбец правых частей.
В работе [4] описано решение подобной системы попеременно треугольным методом, однако результат достигается за значительное число итераций. Медленная сходимость объясняется тем, что низко- и высокочастотные гармоники ошибки ?n на n-м шаге подавляются с одинаковой скоростью и общая сходимость метода определяется лишь крайними границами спектра ошибки.
Для устранения этого недостатка предлагается использовать модифицированную итерационную методику Ричардсона с набором оптимальных значений 
, который обеспечивает поочередное подавление всех гармоник ошибки и её равномерное быстрое уменьшение за небольшое число итераций.
В соответствии с этой методикой значения неизвестных потенциалов un+1 на следующем шаге рассчитываются по схеме
(7)
для наилучшего подавления ошибки за n1 итераций, параметры ?n должны выбираться исходя из условия [2]:
(8)
На практике отыскание набора параметров ?n, минимизирующих норму (8), обычно заменяют отысканием 
, где ?max, ?min – наибольшее и наименьшее собственные числа матрицы A, при которых многочлены Чебышева первого рода степени n1 принимают наиболее близкие к нулю значения. Тогда, как известно [2]:
1 ? n ? n1. (9)
Рассчитанные в соответствии с (9), первые элементы последовательности ?n имеют порядок 1/?max и потому на первых итерациях наиболее активно подавляются гармоники ошибки, соответствующие правой части спектра. Составляющие же левой части спектра гармоники подавляются на этих итерациях медленно. Однако они активно подавляются старшими элементами последовательности ?n, имеющими порядок 1/?min, т.е. при 
Таким образом, происходит значительное равномерное уменьшение ошибки ?n за n1 итераций [2].
Метод Ричардсона характеризуется высокой скоростью сходимости. Известно, что при использовании оптимального набора параметров 
число итераций n на сетке размером N?M узлов зависит от заданной точности ? следующим образом [2]:
(10)
С учетом вышеизложенного программный комплекс «Моделирование МПУ» [4] был модифицирован и с его помощью проведен вычислительный эксперимент МПУ. Обсудим его результаты.
Результаты вычислительного эксперимента и их обсуждение
Результаты моделирования магнитного поля байпасного МПУ накладного типа при фиксированных значениях параметров конструкции (рис. 1) с помощью модифицированного программного комплекса, приведены на рис. 3.
Полученная картина распределения магнитного поля в расчетной области МПУ подтверждается данными других физических и вычислительных экспериментов и соответствует действительности [3–5]. Кроме того, вывод разностных уравнений магнитного поля на основе интегрального тождества обеспечивает наименьшую погрешность аппроксимации.
В функционал программного комплекса была также добавлена возможность подсчета числа итераций, что позволило провести оценку эффективности метода Ричардсона с оптимальным набором параметров ?n, вычисленных по формуле (9). Экспериментальные зависимости числа итераций n от заданной точности ?, полученные при различных наборах параметров ?n, показаны на рис. 4.
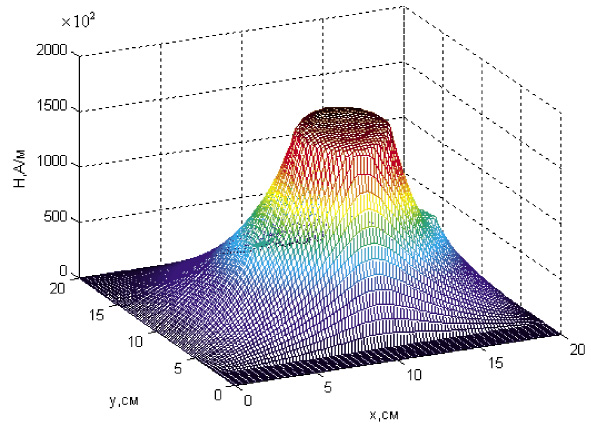
Рис. 3. Напряженность магнитного поля байпасного МПУ накладного типа
Как видно, число итераций n при наборе параметров ?n, рассчитанных по формуле (9) (линия 2), незначительно отличается от идеального теоретического (линия 3), определяемого выражением (10). При случайном выборе набора параметров ?n (линия 1) число итераций возрастает в 2–3 раза.
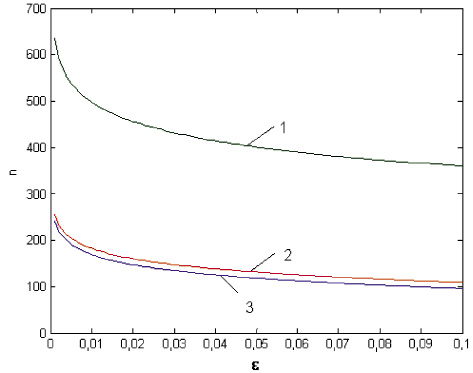
Рис. 4. Влияние набора параметров ?n на число итераций n по методу Ричардсона
На рис. 4 видно, что для достижения точности ? ? 10–3 по модифицированному методу Ричардсона потребуется выполнить n ? 250, что при современных вычислительных ресурсах ЭВМ является вполне приемлемым.
Выводы
Применение метода получения разностных уравнений магнитного поля МПУ накладного типа на основе интегрального тождества позволило сформировать простую методику решения обозначенной задачи, пригодную для применения и в других расчетных областях.
Выбор регулярной сетки при этом минимизирует вычислительную погрешность и дает возможность учесть заданные краевые и граничные условия. Полученная система конечно-разностных уравнений вида (6) полностью описывает распределение магнитного поля в расчетной области МПУ накладного типа, отличается простотой (при реализации вычислительного алгоритма на ЭВМ) и малой погрешностью аппроксимации.
Использование разработанной методики численного расчета магнитных полей МПУ накладного типа для байпасных систем сокращает число итераций и время решения, доказывая её эффективность.
Следует отметить, что разработанный программный комплекс может быть модифицирован для проведения математического моделирования и других магнитострикционных преобразователей с применением других, возможно, более эффективных численных методов. Это достигается за счет модульной структуры программы, при которой алгоритм реализованного численного метода можно легко применить для работы с другими расчетными областями.
Библиографическая ссылка
Карпухин Э.В., Дементьева Е.С., Кулькова Ю.С. СПОСОБ ПОВЫШЕНИЯ ЭФФЕКТИВНОСТИ РАСЧЕТА ПАРАМЕТРОВ МАГНИТОСТРИКЦИОННЫХ ПРЕОБРАЗОВАТЕЛЕЙ УРОВНЯ С ИСПОЛЬЗОВАНИЕМ ПРОГРАММНЫХ КОМПЛЕКСОВ // Фундаментальные исследования. – 2015. – № 12-5. – С. 902-906;URL: https://fundamental-research.ru/ru/article/view?id=39648 (дата обращения: 17.04.2024).