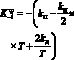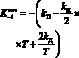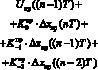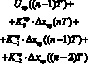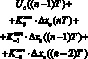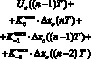При разработке цифровых систем регулирования модель формирования управляющих воздействий на каждом такте регулирования и настроечные параметры регулятора должны подбираться таким образом, чтобы обеспечить требуемые динамические характеристики системы.
Различные математические модели формирования управляющих воздействий (таблица) [1], реализованные в соответствующих алгоритмах, имеют разное количество вычислительных операций и, соответственно, различное время отработки. Для сокращения времени подбора модели и настроечных параметров регулятора необходима оптимизация с унификацией компонентов алгоритма, на основе которых можно осуществлять конструирование новых алгоритмов регулирования. В работе предложен вариант унификации алгоритмов регулирования.
Объектом исследования являются процессы моделирования цифровых регуляторов. Предмет исследования: моделирование цифровых ПИД регуляторов. Цель исследования заключается в унификации алгоритмов для дальнейшего их сравнения и эффективного синтеза алгоритмов цифрового регулирования.
Алгоритмизация дискретных моделей цифрового ПИД регулирования
Изучение дискретных математических моделей цифрового ПИД регулирования (таблица), полученных путем преобразования интеграла и производных в континуальной модели регулирования [1, 4–6]:
![]()
позволило сформулировать соответствующие алгоритмы формирования управляющих воздействий, реализованные в программе оперативной оценки динамики ПИД регулирования (рис. 1) [2]:
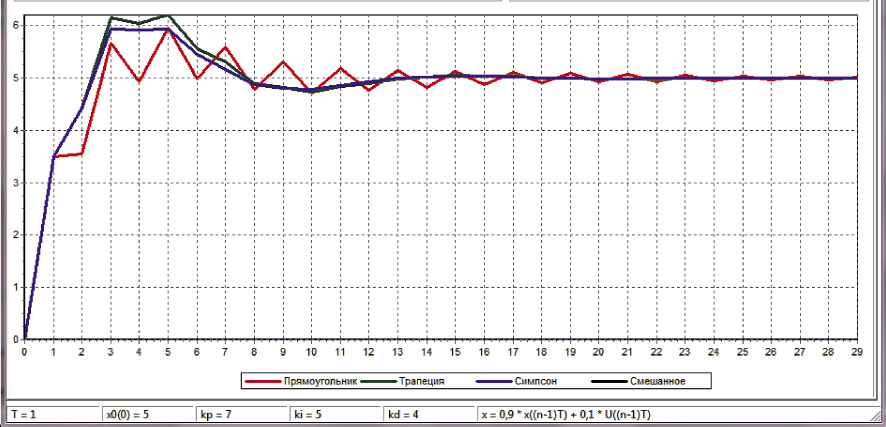
Рис. 1. Программа оперативной оценки динамики ПИД регулирования [2]
Математические модели цифрового ПИД регулирования
|
№ п/п |
Текущий момент времени = nT |
Математическая модель цифрового ПИД регулирования |
|||
|
с раскрытие интеграла по формуле «прямоугольников» Uпp(t) |
с раскрытие интеграла по формуле «трапеций» Uтp(t) |
с раскрытием интеграла по формуле Симпсона Uc(t) |
|||
|
Вспомогательные коэффициенты |
|||||
|
1 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
3 |
|
|
|
|
|
|
4 |
0 |
kПx0 |
kПx0 |
kПx0 |
|
|
5 |
T |
|
|
|
|
|
6 |
2T |
|
|
|
|
|
7 |
(2k + 1)T, k = 1, 2, ... |
|
|||
|
8 |
2kT, k = 2, 3, ... |
|
|||
I. Алгоритм формирования управляющих воздействий на основе модели цифрового ПИД регулирования с раскрытием интеграла по формуле «прямоугольников» (таблица):
1) задание настроечных параметров (kП, kИ, kД) и уставки x0;
2) вычисление коэффициентов ![]()
![]() и
и ![]() ;
;
3) для n = 0, то есть момента времени t = nT = 0?T = 0:
3.1) рассогласование ?пpx(0) = x0;
3.2) формирование управляющего воздействия: Uпp(0) = kПx0;
4) для n =1, то есть момента времени t = nT = 1?T = T:
4.1) вычисление значения рассогласования: ?xпp(T) = x0 – xпp(T);
4.2) вычисление управляющего воздействия:
![]()
5) для момента времени t ? 2T (n ? 2):
5.1) вычисление значения рассогласования в текущий момент времени: ?xтp(nT) = x0 – xтp(nT);
5.2) вычисление управляющего воздействия по формуле
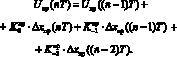
II. Алгоритм вычисления управляющих воздействий по формуле «трапеций» можно сформулировать следующим образом (таблица):
1) задание настроечных параметров (kП, kИ, kД) и уставки x0;
2) вычисление вспомогательных коэффициентов ![]()
![]() и
и ![]() ;
;
3) для n =0, то есть момента времени t = nT = 0?T = 0:
3.1) невязка ?тpx(0) = x0;
3.2) вычисление управляющего воздействия: Uтp(0) = kПx0;
4) для n =1, то есть момента времени t = nT = 1?T = T:
4.1) формирование невязки: ?xтp(T) = x0 – xтp(T);
4.2) вычисление управляющего воздействия:
![]()
5) для момента времени t ? 2T (n ? 2):
5.1) формирование значения невязки: ?xmp(nT) = x0 – xmp(nT);
5.2) вычисление управляющего воздействия:
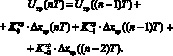
III. Алгоритм формирования управляющих воздействий на основе модели с раскрытием интеграла по формуле Симпсона (таблица):
1) задание настроечных параметров (kП, kИ, kД) и уставки x0;
2) вычисление вспомогательных коэффициентов:
2.1) ![]()
![]() и
и ![]() ;
;
2.2) ![]()
![]() и
и ![]() ;
;
3) для n = 0, то есть момента времени t = nT = 0?T = 0:
3.1) рассогласование ?xc(0) = x0;
3.2) формирование управляющего воздействия: Uc(0) = kПx0;
4) для n = 1, то есть момента времени t = nT = 1?T = T:
4.1) вычисление значения невязки: ?xс(T) = x0 – xс(T);
4.2) вычисление управляющего воздействия по формуле
![]()
5) для момента времени t ? 2T (n ? 2):
5.1) для n = 2, то есть момента времени t = 2T:
5.1.1) вычисление рассогласования: ?xс(2T) = x0 – xс(2T);
5.1.2) вычисление управляющего воздействия по формуле:
![]()
5.2) для n ? 3, то есть момента време ни t ? 3T:
5.2.1) вычисление рассогласования: ?xс(nT) = x0 – xс(nT);
5.2.2) если n = 2k + 1 (k = 1, 2, ...), то вычисление управляющего воздействия по формуле
![]()
5.2.3) если n = 2k, (k = 2, 3, ...), то вычисление управляющего воздействия по формуле
![]()
Унифицированный алгоритм цифрового ПИД регулирования
Исследование дискретных математических моделей цифрового ПИД регулирования (таблица) и соответствующих алгоритмов позволило сформулировать унифицированный алгоритм формирования управляющих воздействий в цифровом ПИД регуляторе (рис. 2):
1) задание настроечных параметров (kП, kИ, kД) и уставки x0;
2) вычисление значений вспомогательных коэффициентов (например, K0, K–1 и K–2) по заданным формулам;
3) для n = 0, то есть момента времени t = nT = 0?T = 0:
3.1) рассогласование ?x(0) = x0;
3.2) формирование управляющего воздействия по формуле U(0) = kПx0;
4) для n = 1, то есть момента времени t = nT = 1?T = T:
4.1) вычисление значения рассогласования ?x(T) = x0 – x(T);
4.2) формирование управляющего воздействия U(T) по заданной формуле;
5) для момента времени t ? 2T (n ? 2):
5.1) вычисление значения рассогласования в текущий момент времени по формуле ?x(nT) = x0 – x(nT);
5.2) формирование управляющего воздействия U(nT) по заданной формуле, например:
![]()
Унифицированный алгоритм (рис. 2) реализован программным инструментарием [3] конструирования алгоритмов цифрового ПИД регулирования (рис. 3).
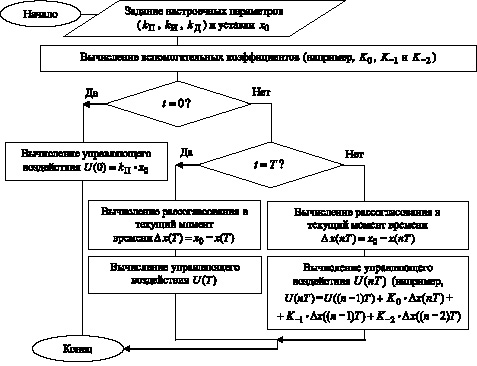
Рис. 2. Унифицированная схема формирования управляющего воздействия в ПИД регуляторе
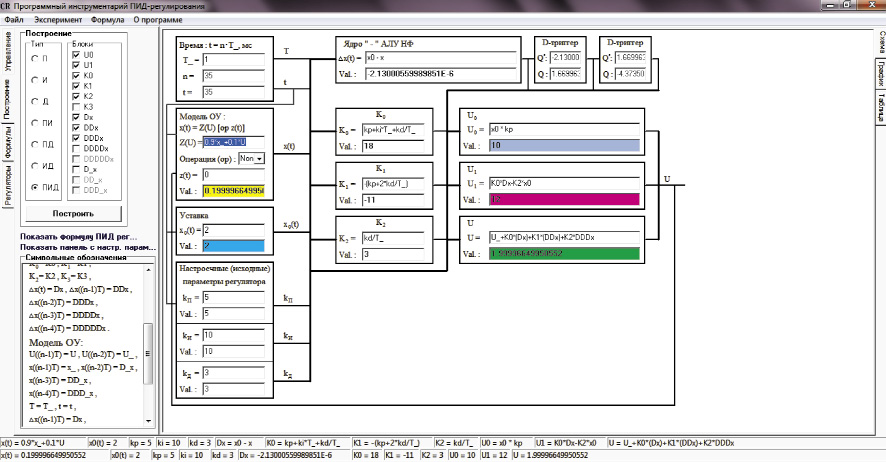
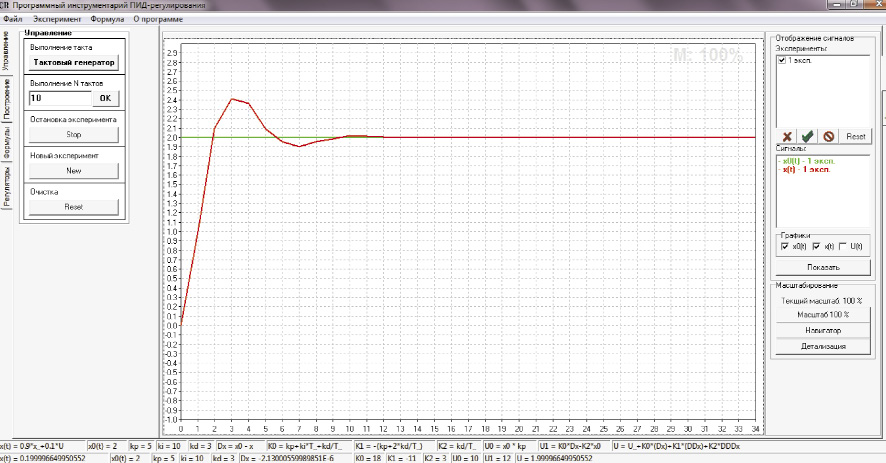
Рис. 3. Программный инструментарий конструирования алгоритмов ПИД регулирования [3]
Основные результаты:
1) предложен новый алгоритм цифрового ПИД регулирования на основе дискретных математических моделей формирования управляющих воздействий, отличающийся унифицированной структурой и оптимальностью формируемых управляющих воздействий;
2) разработан программный инструментарий моделирования процессов цифрового регулирования на базе разработанного алгоритма ПИД регулирования, отличающийся организацией переменной структуры процессов цифрового ПИД регулирования.
Исследование выполнено при поддержке Приокского государственного университета (г. Орел) по теме «Разработка программной системы поддержки процесса управления в предаварийных состояниях для восстановления нормальной работы», приказ № 7-н/26 от 23.10.2013 г.
Библиографическая ссылка
Захарова О.В. УНИФИКАЦИЯ АЛГОРИТМОВ ДЛЯ ЦИФРОВОГО ПИД РЕГУЛИРОВАНИЯ // Фундаментальные исследования. – 2015. – № 12-5. – С. 896-901;URL: https://fundamental-research.ru/ru/article/view?id=39647 (дата обращения: 26.04.2024).