Научный журнал

Фундаментальные исследования

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Жулев Е.Н. 1 Демин Д.Н. 1 Ершов П.Э. 1

---

1 ГБОУ ВПО «Нижегородская государственная медицинская академия» Минздрава России

Целью исследования явилась оценка поведения модели металлокерамического мостовидного протеза с двусторонней опорой под действием разнонаправленной нагрузки и повышение качества протезирования мостовидными протезами при лечении включенных дефектов зубных рядов. С учетом характеристик нами была построена математическая модель металлокерамического мостовидного протеза, опорных зубов, цемента, периодонта и окружающих их десны и костной ткани. При воздействии функциональной нагрузки мы учитывали её направление и оценивали характер смещения и напряжений в этих структурах. Теоретической основой для моделирования деформирования металлокерамического мостовидного протеза и тканей являются методы и подходы теории упругости. Таким образом, полученные результаты позволят врачу оптимизировать выбор конструкции металлокерамического мостовидного протеза и повысить качество лечения пациентов с частичной потерей зубов.

Статья в формате PDF

561 KB

математическая модель

металлокерамический мостовидный протез

функциональная нагрузка

теория упругости

1. Васидзу К. Вариационные методы в теории упругости и пластичности: пер. с англ. – М.: Мир, 1987. – 542 с.

2. Гайворонский И.В., Петрова Т.Б. Анатомия зубов человека. – СПб: ЭЛБИ-СПб, 2005. – 56 с.

3. Жулев Е.Н. Ортопедическая стоматология. – М. : МИА, 2012. – 824 с.

4. Зенкевич О. Метод конечных элементов в технике: пер. с англ. – М.: Мир, 1975. – 536 с.

5. Чуйко А.Н. Еще раз о биомеханике пародонта. Часть 1 // Пародонтология. – 2007 – № 3. – С. 54–60.

6. Чуйко А.Н. Еще раз о биомеханике пародонта. Часть 2 // Пародонтология. – 2007. – № 4. – С. 45–52.

7. Чумаченко Е.Н. Математическое моделирование напряженно-деформированного состояния зубных протезов: учебное пособие / Е.Н. Чумаченко, С.Д. Арутюнов, И.Ю. Лебеденко. – М.: Молодая Гвардия, 2003. – 272 с.

В настоящее время большое внимание клиницистов приковано к ортопедическому лечению включенных дефектов зубных рядов с помощью металлокерамических мостовидных протезов. В то же время накопленный клинический опыт показывает, что этот метод лечения весьма далек от совершенства. Особенно это относится к вопросам планирования конструкции металлокерамического протеза при различных клинических условиях, обусловленных прежде всего протяженностью дефекта зубного ряда, размерами клинических коронок естественных зубов и их положением на альвеолярном отростке, состоянием пародонта и беззубой альвеолярной части, соотношением оставшихся зубов, видом прикуса и т.д. [3]. Особую роль играет применение метода математического моделирования при анализе биомеханики протезов, а также создание программ компьютерного моделирования, позволяющих построить и проанализировать биомеханические свойства конструкций [1]. Важное место в решении практических задач ортопедической стоматологии занимает исследование характера распределения упругих напряжений в тканях пародонта опорных зубов под воздействием протезов. Дополнительно возникающие напряжения при использовании несъемных мостовидных протезов вызывают перегрузку опорных зубов, что ведет к дистрофии пародонта, клинически проявляющейся в виде патологической подвижности зубов, к обнажению шейки зуба и к вторичному перемещению зубов [7]. Учет факторов, способствующих напряжению в металлокерамических мостовидных протезах, позволит значительно повысить качество ортопедического лечения и уменьшить число осложнений.

Цель исследования – изучение распределения смещения и напряжений в металлокерамическом мостовидном протезе с двусторонней опорой под воздействием разнонаправленной нагрузки.

Материал и методы исследования

Для исследования была создана математическая модель металлокерамического мостовидного протеза с опорой на зубы 34, 37. Модель включала в себя челюстную кость, опорные зубы, периодонт и конструкцию протеза. Модель изготавливали как геометрически подобную реальной системе. Физические свойства материалов и тканей, задаваемые в математической модели, были взяты из справочной литературы и приведены в таблице.

При построении математической модели за основу принимались геометрические данные, полученные сканированием зубного ряда больного. Затем из зубного ряда вырезались данные, относящиеся к изучаемым зубам, и переносились в программный пакет Rhinoceros 4.0. Для построения модели использовались методы сплайн-аппроксимаций. Для этого в Rhinoceros 4.0 импортировался набор точек, на который затем накладывалась сплайновая поверхность. Построенная таким образом часть модели хорошо повторяет все элементы жевательной поверхности зуба. Для построения модели однокоренного зуба вначале строились опорные линии. Затем на край жевательной поверхности и опорные линии накладывалась поверхность. Аналогично строились поверхности, моделирующие корень и препарированную часть зуба. Размеры и геометрические формы зубов выбирались на основе эскизов и атласов [2]. Внешняя поверхность периодонта создавалась как равноотстоящая от поверхности зубного корня на 0,1 мм. Внутренняя поверхность совпадает с поверхностью зуба, внешняя повторяет форму лунки. Окружающая костную ткань десна создаётся таким же образом, и с помощью готовых моделей периодонта формируются лунки для зубов.

Построение модели протеза начиналось с модели цементного слоя. Внутренняя поверхность цемента совпадает с препарированной поверхностью зуба. Внешняя поверхность цемента строилась как отстоящая от внутренней поверхности на заданное расстояние (0,1 мм). Внешние поверхности металлических коронок создавались согласно принятой технологии по опорным линиям. Модели базиса протезов отсутствующих зубов также создавались по принятой технологии по эскизам. После этого все элементы металлического базиса соединялись между собой. Керамический слой строился по тому же методу. За внешнюю поверхность керамики брались внешние поверхности зубов, построенные ранее. Внутренняя поверхность совпадает с внешней поверхностью металлического базиса металлокерамического мостовидного протеза. При соединении всех элементов используется гладкое сопряжение поверхностей. Таким образом построены все элементы модели: опорные зубы, периодонт, челюстная кость, цементный слой, металлический базис, керамическое покрытие.

Созданные геометрические модели экспортировались в программный пакет ANSYS, где строилась конечно-элементная сетка и задавались нагрузки. Функциональная нагрузка равномерно распределялась по всей жевательной поверхности металлокерамического мостовидного протеза. Боковая нагрузка прикладывалась перпендикулярно зубному ряду в язычном и щечном направлениях. Теоретической основой для моделирования деформаций протеза и тканей являются методы и подходы теории упругости. Для оценки опасности напряженного состояния применяются так называемые эквивалентные напряжения. Для металлов и сплавов в качестве эквивалентного напряжения традиционно используется интенсивность напряжений. Однако есть основания полагать [7], что состояние живых тканей зависит и от изменения объема и от знака напряжений. В связи с этим [7] для оценки биомеханической естественно-искусственной системы «челюсть – зубы – протез» мы использовали критерий Шлейхера – Надаи, зависящий от интенсивности касательных напряжений и величины среднего или гидростатического давления.

Данное биомеханическое исследование посвящено сравнительному анализу влияния различных вариантов крепления зубного протеза на напряженное состояние в тканях и элементах протеза. Для сравнения и анализа работы системы «челюсть – зубы – протез» мы использовали две величины: интенсивность напряжений (или напряжение по Мизесу), характеризующее энергию изменения формы, и среднее (или гидростатическое) напряжение. Для оценки напряженного состояния хрупких сред, таких как цемент или керамика, применяли критерий максимальных растягивающих напряжений.

Результаты исследования и их обсуждение

В результате нашего исследования поведения математической модели металлокерамического мостовидного протеза с опорой на зубы 34 и 37 мы получили следующие результаты. При изучении перемещений по осям при воздействии нагрузкой наибольшее перемещение в горизонтальной плоскости (оси X и Y) испытывают бугры как опорных, так и искусственных зубов мостовидного протеза. При язычном направлении вертикальной силы максимальное смещение по оси Z испытывает щечная стенка опорного второго моляра, а также смещаются ткани вестибулярной поверхности альвеолярной части в области второго моляра (рис. 1). При язычно-щечном направлении вертикальной силы максимальное смещение по оси Z испытывает металлокерамический мостовидный протез в области щечных стенок опорного первого премоляра, искусственного второго премоляра и искусственного первого моляра.

Кроме смещения по осям нами было изучено суммарное смещение в металлокерамическом мостовидном протезе. При язычном направлении вертикальной силы максимальное суммарное смещение локализуется на щечных и язычных бугорках премоляров, мезиально-щечных и мезиально-язычных бугорках первого моляра. При действии вертикальной силы в щечном направлении максимальное суммарное смещение испытывают щечные бугорки премоляров и небольшой участок на мезиально-щечном бугорке искусственного первого моляра.

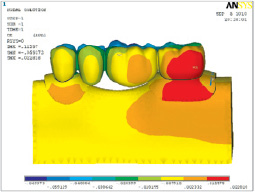
Рис. 1. Смещение по оси Z в модифицированной модели мостовидного протеза при действии силы в язычном направлении (вид со щечной поверхности)

Мы изучили каждый компонент металлокерамического мостовидного протеза в отдельности. По результатам математического моделирования поведения тканей опорного премоляра под воздействием функциональной нагрузки мы получили данные интенсивности напряжения (напряжения по Мизесу) и гидростатического давления. При язычном и щечном направлении вертикальной силы максимальная интенсивность напряжений концентрируется в пришеечной области зуба с дистальной стороны. При язычном направлении вертикальной силы максимальное объёмное растяжение величиной в 5,77 МПа испытывает вестибулярная поверхность корня зуба. При щечном направлении вертикальной силы объёмное растяжение величиной 2,4 МПа испытывает не только язычная поверхность корня, но и культя подготовленного под металлокерамический мостовидный протез премоляра. При этом объёмное сжатие локализуется на дистальной поверхности в области уступа подготовленного под металлокерамический мостовидный протез зуба (рис. 2).

Второй опорный моляр мы изучили по тем же показателям. При язычном направлении вертикальной силы максимальные напряжения по Мизесу испытывает пришеечная область зуба с мезиальной поверхности, тогда как при щечном направлении вертикальной силы напряжена пришеечная область зуба с дистальной стороны. Объемное растяжение при щечно-язычном направлении вертикальной силы испытывает пришеечная область мезиального корня зуба с мезиальной стороны. При этом гидростатическое давление рассеивается на мезиальном и дистальном корнях моляра, и становится равномерным на культе подготовленного под металлокерамический мостовидный протез моляра. На мезиальной поверхности в области уступа подготовленного под металлокерамический мостовидный протез зуба, а также в верхней трети апроксимальной поверхности мезиального корня ткани зуба испытывают объёмное растяжение.

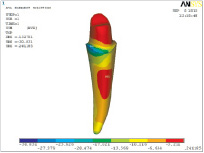
Рис. 2. Гидростатическое или среднее (по трём осям) давление в тканях премоляра при щечном направлении вертикальной силы

По результатам математического моделирования поведения периодонта премоляра под воздействием функциональной нагрузки при язычном направлении вертикальной силы максимальные эквивалентные напряжения испытывает дистальная поверхность пришеечной трети периодонта. При язычном направлении вертикальной силы объёмное растяжение испытывает щечная поверхность пришеечной трети периодонта в области зубодесневого соединения, объемное сжатие локализуется на мезиальной поверхности пришеечной трети периодонта и так же в области зубодесневого соединения и периодонта верхушки зуба.

Математическое моделирование поведения периодонта моляра под воздействием функциональной нагрузки при язычном направлении вертикальной силы показало, что максимальные эквивалентные напряжения величиной 6,1 МПа испытывает язычная поверхность пришеечной трети периодонта мезиального корня опорного моляра. При язычном направлении вертикальной силы объемное растяжение испытывает щечная поверхность пришеечной трети периодонта в межкорневой области, а также периодонт в области верхушки дистального корня. Объемное сжатие величиной 4,6 МПа испытывает межкорневая часть периодонта с язычной поверхности и верхняя треть дистального корня. При направлении вертикальной силы щечно-дистальная поверхность пришеечной трети периодонта испытывает объемное растяжение, объемное сжатие – периодонт в межкорневой части со щечной поверхности, а также в области верхушки мезиального корня (рис. 3).

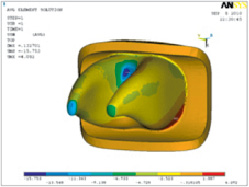
Рис. 3. Гидростатическое давление в периодонте моляра при щечном направлении вертикальной силы

Затем мы изучили воздействие нагрузки на десну в области металлокерамического мостовидного протеза. При щечном направлении вертикальной силы максимально напряжена десна щечной поверхности премоляра (35 МПа), при этом минимальные эквивалентные напряжения превалируют на десне, покрывающей гребень альвеолярной части, и в области лунок корней опорного моляра.

По результатам математического моделирования поведения цемента растягивающие напряжения в цементе распределяются сходно при разных направлениях функциональной нагрузки: максимально напряжен цемент дистальной поверхности. При щечном направлении вертикальной силы максимальные растягивающие напряжения испытывает цемент с язычной поверхности уступа, подготовленного под металлокерамический мостовидный протез зуба.

Рис. 4. Максимальное растягивающее напряжение в керамике при действии вертикальных сил в щечно-язычном направлении, обзор металлокерамического мостовидного протеза с щечной поверхности в области соединения искусственных зубов

Математическое моделирование поведения керамики металлокерамического мостовидного протеза под воздействием функциональной нагрузки дало следующие результаты. Как видно на рис. 4, при язычном и щечном направлениях вертикальной силы максимальные растягивающие напряжения испытывает межзубная область в промежуточной части керамики металлокерамического мостовидного протеза между искусственными премоляром и моляром.

При язычном и щечном направлении вертикальной силы на металлический базис мостовидного протеза максимальные напряжения по Мизесу испытывает межзубная область опорного первого премоляра и искусственного второго моляра металлического каркаса металлокерамического мостовидного протеза, а также соединение между искусственными премоляром и моляром и дистальная поверхность металлического каркаса коронки первого премоляра (рис. 5).

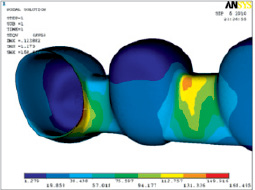
Рис. 5. Эквивалентные напряжения в металлическом базисе металлокерамического мостовидного протеза при действии вертикальных сил в язычно-щечном направлении, обзор металлокерамического мостовидного протеза с нижней стороны в области соединения искусственных зубов и опорного и искусственного премоляров

Заключение

При различных направлениях нагрузки, оказываемой на металлокерамический мостовидный протез с опорами на зубы 35, 37, наибольшему смещению подвержены бугорки опорных и искусственных зубов металлокерамического протеза. При изучении напряжения в керамике и металлическом каркасе мостовидного протеза максимально напряжены межзубные части его составляющих. Таким образом, учет полученных результатов позволит врачу оптимизировать выбор конструкции металлокерамического мостовидного протеза и повысить качество лечения пациентов с частичной потерей зубов.

Дурново Е.А., д.м.н., профессор, зав. кафедрой хирургической стоматологии и челюстно-лицевой хирургии, ГБОУ ВПО «Нижегородская государственная медицинская академия» Минздрава России, г. Нижний Новгород;

Казарина Л.Н., д.м.н., профессор, зав. кафедрой пропедевтической стоматологии, ГБОУ ВПО «Нижегородская государственная медицинская академия» Минздрава России, г. Нижний Новгород.

Работа поступила в редакцию 29.12.2014.

Библиографическая ссылка