Важным направлением сейсмологических исследований является использование различных закономерностей в поведении сейсмичности в предыдущие моменты времени для прогнозирования будущих землетрясений. Наиболее часто используемой закономерностью является снижение сейсмической активности (или сейсмическое затишье) перед сильным землетрясением.
В сейсмогенных зонах происходит накопление напряжений под действием тектонических деформаций. Снижение сейсмической активности свидетельствует об отсутствии разрядки (сброса) накопленных напряжений. Когда накопленные напряжения превосходят предел прочности среды, происходит землетрясение. Чем больше этот предел прочности, тем дольше будут накапливаться напряжения и тем сильнее будущее землетрясение. Логично предположить, что сейсмическое затишье является индикатором того, что напряжения в среде накапливаются в течение длительного времени, что является предпосылкой для возникновения сильного землетрясения. Отметим, что не всегда сброс накопленных напряжений происходит в виде землетрясения. Для землетрясения необходимо, чтобы напряжения сбрасывались довольно быстро.
Афтершоковый процесс является частным случаем сейсмической активности, которая возникает, если после сильного землетрясения, называемого основным толчком, происходит восстановление поля напряжений в зоне разрыва. Поскольку афтершоковый процесс характеризует напряженное состояние среды [6], то соображения, изложенные выше, применимы и к возникновению сильных афтершоков.
К настоящему времени предложен ряд методик для оценки сейсмического затишья. Например, методика RTL (Region-Time-Length), предложенная Г.А. Соболевым [5], основана на вычислении одноименной величины, зависящей от трех составляющих сейсмического режима: расстояние (R), время (T) и длина разрыва (L). Выход величины RTL на отрицательные значения сигнализирует о начале сейсмического затишья, которое является предвестником землетрясения. Эффективность методики RTL при прогнозировании сильных землетрясений Камчатки варьируется от 53 до 80 % в зависимости от магнитуды [4]. Отметим, что поскольку RTL-методика использует данные, из которых были предварительно исключены афтершоки, она больше подходит для прогнозирования основных толчков, чем афтершоков.
Подходом, использующим сейсмическое затишье в качестве предвестника именно сильных афтершоков, является методика, основанная на анализе отклонений кумулятивной кривой, полученной по ETAS-модели от фактической кумулятивной кривой [9]. ETAS-модель оценивается на базисном интервале и экстраполируется на прогнозный интервал. Если фактическая кривая опускается ниже модельной кривой, то имеет место сейсмическое затишье, которое является предвестником сильного афтершока. Недостатки методики:
1) предвестник является ошибкой прогноза, а не следствием соответствия модели исходным данным;
2) ограниченность используемой информации для оценки параметров ETAS-модели (после интервала, где оцениваются параметры модели, должно пройти еще некоторое время, достаточное для оценивания значимости отклонений модели от фактических данных, и только после этого принимается решение о возможном сильном афтершоке).
В настоящей работе автор предлагает свой вариант понятия «активность афтершокового процесса», которое является вероятностью того, что на некотором интервале произойдет сильное землетрясение, которое является афтершоком, а не фоновым событием. При приближении значения активности к 0 имеет место сейсмическое затишье, а при приближении к 1 – активизация. Вычисление активности афтершокового процесса основано на совместном использовании закона Гутенберга ‒ Рихтера и ETAS-модели.
В качестве примера приводится вычисление активности для афтершоковых процессов трех сильных землетрясений из районов с различным сейсмогенезом (Камчатка, Алтае-Саянская складчатая область и Северный Кавказ). Показано, что для рассматриваемых афтершоковых последовательностей сейсмическое затишье является предвестником сильных событий.
Описание методики
Прежде чем преступить к изложению методики, необходимо формализовать понятие сильного землетрясения. Под сильным землетрясением на временном интервале (S, T) будем понимать такое землетрясение, магнитуда которого больше магнитуды 95 % землетрясений, произошедших на этом интервале. Магнитуду, начиная с которой землетрясение является сильным, назовем пороговой магнитудой.
Предположим, что магнитуды афтершоков независимы и одинаково распределены. Тогда согласно закону Гутенберга ‒ Рихтера (lgN = a – b·M [8]) распределение магнитуд сейсмических событий имеет вид [12]:
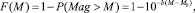 (1)
(1)
где b – параметр закона Гутенберга ‒ Рихтера; M0 – магнитуда выборки, не меньшая магнитуды представительности [13].
Интенсивность афтершокового процесса на временном интервале (S, T) по ETAS-модели сейсмичности имеет вид [9]:
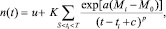 (2)
(2)
где u – значение фоновой сейсмичности (среднее число землетрясений в единицу времени); t – время после основного толчка; ti – время, Mi – магнитуда i-го афтершока; M0 – магнитуда выборки, не меньшая магнитуды представительности; c, p, K, a – подлежащие определению параметры модели, которые одинаковы для всех событий, произошедших на временном интервале (S, T).
Фоновая сейсмичность u в (2) описывает сейсмическую активность, которая не является частью афтершокового процесса [9].
Суть предлагаемой автором методики заключается в оценивании параметров закона Гутенберга-Рихтера и ETAS-модели в движущемся временном окне с целью вычисления вероятности того, что сейсмическое событие не является фоновым и является сильным (его магнитуда будет больше, чем магнитуда 95 % событий из временного окна).
Пусть M1(t) – пороговая магнитуда во временном окне (t – w, t), w – ширина окна. Тогда, согласно (1), вероятность того, что хотя бы одно событие будет иметь магнитуду большую, чем пороговая, имеет вид
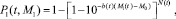 (3)
(3)
где b(t) – параметр закона Гутенберга ‒ Рихтера на интервале (t – w, t); N(t) – количество землетрясений, произошедших на интервале (t – w, t). Второе слагаемое в (3) задает вероятность того, что все N(t) событий, произошедших в окне (t – w, t), имеют магнитуды меньше, чем M1(t). Вычитая это значение из 1, мы получим вероятность того, что хотя бы одно событие будет иметь магнитуду больше, чем M1(t).
Пусть u(t) – значение фоновой сейсмичности (число событий в единицу времени), оцененное с помощью ETAS-модели (2), во временном интервале (t – w, t). Тогда количество фоновых событий, произошедших на данном интервале, равно произведению u(t) и ширины окна w. Вероятность того, что событие не является фоновым, задается соотношением
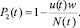 (4)
(4)
Под сейсмической активностью афтершокового процесса на интервале времени (t-w, t) будем понимать вероятность того, что на этом интервале произойдет хотя бы одно сильное землетрясение, которое не является фоновым. Определенная таким образом сейсмическая активность задается произведением вероятностей, вычисленных по формулам (3) и (4):
P(t) = P1(t,M1)·P2(t), (5)
где M1 = M1(t) – пороговая магнитуда во временном окне (t – w, t).
Если значение вероятности P(t) близко к 1, то на временном интервале (t – w, t) наблюдается сейсмическая активизация; если же значение P(t) близко к 0 – сейсмическое затишье.
При вычислении активности афтершокового процесса (5) в некоторый момент времени используются времена и магнитуды событий, произошедших до этого момента. Это свойство является важным, поскольку позволяет использовать особенности поведения активности для выявления предвестников сильных афтершоков.
Примеры расчета афтершоковой активности
В качестве примеров приведем расчеты активности для 3 афтершоковых процессов сильных землетрясений из районов с различным типом сейсмогенеза:
1. Землетрясение у Юго-восточного побережья Камчатки, 08.06.1993 в 13:03:37 (UT – мировое время), магнитуда основного толчка ML = 6,8, координаты эпицентра: 51,2° с.ш. и 175,8°в.д.; число афтершоков, произошедших за 7 суток, – 118; магнитуда представительности M0 = 3,5.
2. Первое Тувинское землетрясение (Алтае-Саянская складчатая область), 27.12.2011 в 15:21:55 (UT), магнитуда основного толчка ML = 6,3, координаты эпицентра: 51,744° с.ш. и 95,823°в.д.; число афтершоков, произошедших за 7 суток – 307; магнитуда представительности M0 = 2.
3. Рачинское землетрясение (Северный Кавказ), 04.29.1991 в 09:12:46 (UT), магнитуда основного толчка ML = 6,9, координаты эпицентра: 42,390° с.ш. и 43,680° в.д.; число афтершоков, произошедших за 7 суток – 469; магнитуда представительности M0 = 2,5.
Отметим, что афтершоковые последовательности данных землетрясений хорошо изучены [1–3].
Активность (5) рассчитывалась по данным за первые 7 суток после основного толчка. Выбор начальной стадии афтершоковой последовательности для иллюстрации понятия активности процесса обусловлен тем, что сильные афтершоки происходят, как правило, в начале афтершоковой последовательности и медианное значение времени между основным толчком и сильнейшим афтершоком составляет примерно 3 суток [11]. Кроме того, именно в первые сутки после сильного землетрясения важно начать спасательные работы, организация которых должна учитывать возможность возникновения сильных афтершоков.
При расчетах активности афтершокового процесса по формуле (5) ширина окна w равнялась 0,5 суток (12 часов), на каждом шаге окно сдвигалось на 0,125 суток (3 часа). Параметр b в законе Гутенберга ‒ Рихтера оценивался принятым в сейсмологии методом максимального правдоподобия [7]. Оценивание параметров ETAS-модели также выполнялось методом максимального правдоподобия [10].
Результаты расчетов представлены на рисунке: верхние графики – зависимость магнитуды афтершоков от времени (черная кривая – пороговая магнитуда, которую превосходят 5 % событий в временном окне (t – w, t)), нижние графики – активность афтершокового процесса, рассчитанная по формуле (5). На нижних графиках горизонтальная черная прямая соответствует вероятности 10 %, того, что во временном окне (t – w, t) событие не является фоновым и его магнитуда больше пороговой.
Расчеты показывают, что для всех рассматриваемых основных толчков перед сильными афтершоками наблюдается снижение активности афтершокового процесса (5). Если принять, что при значениях активности P(t) меньших, чем 0,1, имеет место затишье, можно заметить, что сильные афтершоки происходят либо во время затишья, либо сразу после него (рисунок). Таким образом, спад активности афтершокового процесса (5) можно рассматривать как предвестник сильных афтершоков. Предложенная методика позволяет зафиксировать этот спад.
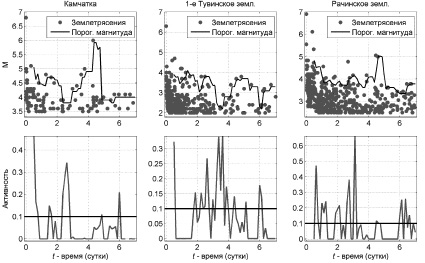
а б в
Зависимость магнитуды афтершоков от времени (верхние графики) и активность афтершокового процесса (нижние графики, горизонтальная черная прямая соответствует 10 %-й вероятности), рассчитанная по формуле (5). Ноль на горизонтальной оси соответствует времени основного толчка
Заключение
В работе предложено авторское определение активности афтершокового процесса, которое является вероятностью того, что на некотором интервале произойдет сильное землетрясение, которое является афтершоком, а не фоновым событием. Вычисление активности основано на использовании закона Гутенберга ‒ Рихтера и ETAS-модели. Закон Гутенберга ‒ Рихтера используется для характеристики сейсмического режима афтершокового процесса в некоторый момент времени, ETAS-модель – для оценки сейсмичности, не являющейся частью афтершокового процесса.
Результаты расчета активности для афтершоковых процессов трех сильных землетрясений из районов с различным сейсмогенезом (Камчатка, Алтае-Саянская складчатая область, Северный Кавказ) показали, что сильные афтершоки происходят либо во время спада активности (затишье), либо сразу после его окончания.
Таким образом, фиксируемый методикой спад сейсмической активности может использоваться в работе центров сейсмического мониторинга после сильного землетрясения как предвестник сильных афтершоков.
Работа выполнена при поддержке РФФИ (проект № 13-05-00158).
Рецензенты:Скуфьин П.К., д.г.-м.н., ведущий научный сотрудник, ФГБУН «Геологический институт» Кольского научного центра Российской академии наук, г. Апатиты;
Олейник А.Г., д.т.н., заместитель директора по научной работе, ФГБУН «Институт информатики и математического моделирования технологических процессов» Кольского научного центра Российской академии наук, г. Апатиты.
Работа поступила в редакцию 16.12.2014.
Библиографическая ссылка
Баранов С.В. ОЦЕНКА АКТИВНОСТИ АФТЕРШОКОВОГО ПРОЦЕССА С ПОМОЩЬЮ ЗАКОНА ГУТЕНБЕРГА ‒ РИХТЕРА И ETAS-МОДЕЛИ // Фундаментальные исследования. – 2014. – № 12-4. – С. 751-755;URL: https://fundamental-research.ru/ru/article/view?id=36182 (дата обращения: 20.04.2024).



