Транспортирование измельченных твердых материалов в трубопроводах при помощи потока воздуха – пневмотранспортирование – широко используется в промышленности.
Существующие методы расчета характеристик пневмотранспортных установок основаны, как правило, на эмпирических зависимостях, выявленных при экспериментальных исследованиях движения различных сыпучих материалов в различных условиях. Коэффициенты, входящие в эмпирические зависимости, у разных авторов различаются, и применение методов расчета ограничено теми диапазонами условий пневмотранспортирования, при которых проводились эксперименты. Экспериментальные исследования при других условиях движения сыпучих материалов требуют создания новых установок, их проведение сложно, длительно и дорогостояще. Практика создания пневмотранспортных систем ставит задачу разработки методики их инженерного расчета. Такая методика должна быть пригодной для расчета систем при различных условиях пневмотранспортирования материалов. Использование в исследованиях процессов пневматического транспортирования методов математического моделирования позволяет уменьшить затраты на разработку методик расчета гидравлического сопротивления участков пневмотранспортных установок, в частности трубопроводов. Следует отметить, что еще недостаточно изучено турбулентное движение даже чистого воздуха в трубопроводах. Однако определение гидравлического сопротивления трубопроводов при движении чистого воздуха представляет собой все же менее сложную проблему, чем при транспортировании воздухом сыпучих материалов.
Падение давления воздуха в трубопроводе, в котором транспортируется сыпучий материал, вычисляют по формуле Дарси – Вейсбаха [3]:
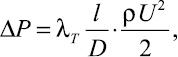 (1)
(1)
где ΔР – падение давления воздуха в трубопроводе, λТ – коэффициент сопротивления единицы относительной длины трубопровода движению воздуха и взвешенных твердых частиц; l, D – длина и внутренний гидравлический диаметр трубопровода; ρ – плотность воздуха; U – средняя скорость воздуха по сечению трубопровода, рассчитываемая как отношение объемного расхода воздуха к площади поперечного сечения трубопровода.
Для концентраций частиц достаточно больших, чтобы можно было пренебречь их влиянием на сглаживание пульсаций скорости воздуха («эффект Томса» [3]), экспериментально определено, что имеет место соотношение [2, 6]:
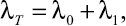 (2)
(2)
где λ0 и λ1 – коэффициенты сопротивления единицы относительной длины трубопровода соответственно движению чистого воздуха и движению взвешенных твердых частиц. Величина λ1 пропорциональна массовому расходу частиц через сечение трубопровода m [2, 6].
Целью исследования явилось теоретическое определение зависимости λ1 от внутреннего диаметра трубопровода, расхода твердых частиц, скорости движения частиц, плотности, вязкости и скорости воздуха, а следовательно, и падения давления воздуха в горизонтальном трубопроводе при пневмотранспортировании твердых частиц в непрерывном режиме.
В качестве метода исследования использовано математическое моделирование взаимодействия частиц с воздушным потоком в трубопроводе. Рассмотрено установившееся пневмотранспортирование сыпучего материала – твердых частиц сферической формы – на прямом горизонтальном участке трубопровода. Предполагалось, что диаметры частиц превышают длину свободного пробега молекул дисперсионной среды (воздуха) и теплообмен между газовзвесью и окружающей средой отсутствует. Поток рассматривается стационарным. Это значит, что скорость воздуха, его плотность, скорость частиц и их концентрация не меняются при переходе от одного сечения трубопровода к другому.
Пусть ΔР0 – падение давления чистого воздуха (не несущего поток твердых частиц) при его движении со средней скоростью U. Из соотношений (1) и (2)
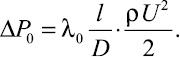 (3)
(3)
В дальнейшем зависимость λ0 от скорости движения воздуха, его плотности и вязкости, от шероховатости стенок трубопровода и его внутреннего диаметра считается известной.
При движении воздуха, несущего твердые частицы, произведение падения давления воздуха и площади поперечного сечения равно сумме сил, действующих на воздух со стороны движущихся частиц, и силы трения, действующей на воздух со стороны стенок трубы. Последнюю силу вследствие малого количества частиц можно считать равной силе при движении чистого воздуха в трубопроводе. Из этого следует, что
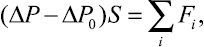 (4)
(4)
где S – площадь поперечного сечения трубопровода; Fi – величина проекции на ось трубопровода силы, действующей со стороны воздуха на i-ю частицу, а суммирование в правой части соотношения производится по всем частицам, находящимся на участке трубопровода длиной l. В случае, когда скорость частицы меньше скорости движения воздуха, величина Fi положительна, а когда больше – отрицательна.
Величина Fi для сферических частиц определяется следующим равенством:
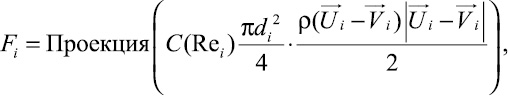 (5)
(5)
где di – диаметр i-й частицы; Ui – скорость воздуха в месте нахождения частицы; Vi – скорость движения частицы; C(Rei) – коэффициент сопротивления частицы, зависящий от числа Рейнольдса
[1, 4, 5, 7]:
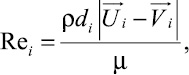 (6)
(6)
где μ – коэффициент динамической вязкости воздуха.
Из соотношения (4) с учетом (1)–(3) и (5) получаем
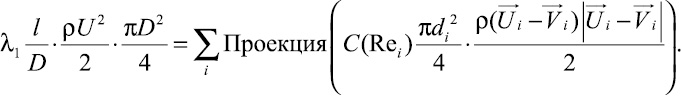 (7)
(7)
Для монодисперсных сферических частиц, заменяя в соотношении (7) разницу в скорости воздуха и частиц на среднее значение, имеем
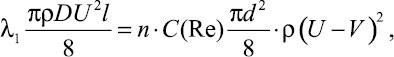 (8)
(8)
где n – число частиц на участке трубопровода длиной l.
Из последнего соотношения получаем
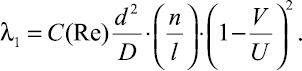 (9)
(9)
Величина n/l равна количеству частиц, приходящемуся на единицу длины трубопровода.
Расход частиц равен следующей
величине
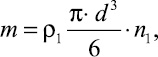 (10)
(10)
где m – массовый расход частиц; ρ1 – плотность частиц; n1 – число частиц, поступающих в трубопровод в единицу времени (количественный расход частиц). Величина n1 связана с n следующим соотношением
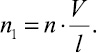 (11)
(11)
Из (10) и (11) следует, что
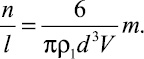 (12)
(12)
С учетом последнего равенства из соотношения (9) следует выражение для коэффициента сопротивления
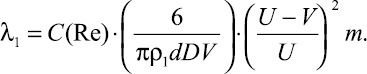 (13)
(13)
В том случае, когда Re < 1, коэффициент сопротивления частицы можно рассчитать по формуле [1, 4, 7]:
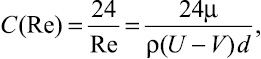 (14)
(14)
и тогда
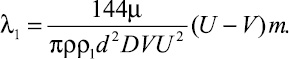 (15)
(15)
При (U – V) << U
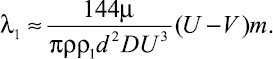 (16)
(16)
При выводе соотношений для изменения перепада давления воздуха вследствие запыленности потока предполагали, что скорость движения частиц меньше, чем скорость воздуха. В том случае, если это не так (это может иметь место, например, при движении частиц при расширении трубопровода), перепад давления воздуха, несущего частицы, будет меньше на величину λ1ρU2l/(2D) перепада давления чистого воздуха, движущегося с той же скоростью, что и воздух, несущий частицы.
Соотношения для коэффициента λ1, полученные выше в предположении одинаковой скорости движения частиц, распространяются на пневмотранспортирование частиц, имеющих разные скорости. Если f(V) – плотность функции распределения частиц по скорости, то вместо соотношений (13), (15), (16) для расчета коэффициента сопротивления единицы относительной длины трубопровода движению взвешенных твердых частиц следует использовать соответственно следующие формулы:
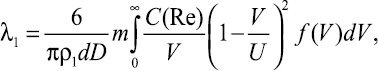 (17)
(17)
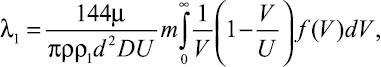 (18)
(18)
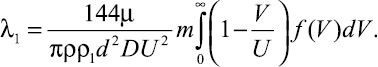 (19)
(19)
Предварительная апробация этих соотношений на ряде экспериментальных данных показала, что расчетные значения падения давления воздуха при движении газовзвесей удовлетворительно согласуются с опытными данными.
Таким образом, получены соотношения для коэффициента сопротивления трубопровода движению взвешенных сферических твердых частиц, а также частные соотношения для этого коэффициента при стоксовском режиме обтекания частиц потоком воздуха. Эти соотношения, после выявления зависимости скорости движения частиц от скорости воздуха и параметров трубопровода, могут быть положены в основу методики расчета непрерывного горизонтального пневмотранспорта сыпучих материалов.
Рецензенты:Флегентов И.В., д.т.н., профессор, заведующий кафедрой промышленной экологии и безопасности, Вятский государственный университет, г. Киров;
Кучеренко А.С., д.т.н., доцент, главный научный сотрудник филиала ФГБУ
«48 Центральный научно-исследовательский институт» Министерства обороны Российской Федерации, г. Киров.
Работа поступила в редакцию 28.11.2014.
Библиографическая ссылка
Крючков А.В., Лещенко А.А. ПАДЕНИЕ ДАВЛЕНИЯ ВОЗДУХА ПРИ ПНЕВМОТРАНСПОРТИРОВАНИИ ТВЕРДЫХ ЧАСТИЦ // Фундаментальные исследования. – 2014. – № 11-12. – С. 2589-2592;URL: https://fundamental-research.ru/ru/article/view?id=36027 (дата обращения: 25.04.2024).



