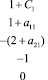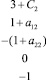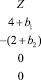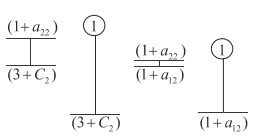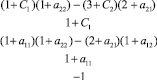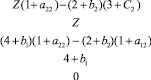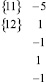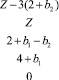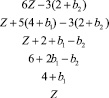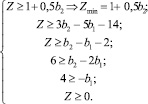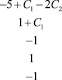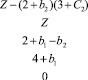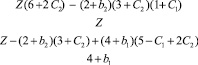Научный журнал

Фундаментальные исследования

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Кравчук С.П. 1 Кравчук И.С. 2 Татарников О.В. 1 Швед Е.В. 1

---

1 ГОУ ВПО «Российский экономический университет им. Г.В. Плеханова»

2 ФГБОУ ВПО «Московский государственный университет путей сообщения»

При анализе инженерных и экономических проблем, которые сводятся к задачам линейного программирования, зачастую необходимо проводить исследование математической модели на чувствительность к изменению в определенном интервале коэффициентов задачи. Такое изменение коэффициентов может быть представлено в виде их зависимости от некоторого параметра. При использовании симплекс-метода подобный анализ является трудоемким процессом, поскольку требует нахождения оптимальных решений для каждого набора значений изменяемых коэффициентов. В данной работе предлагается метод решения задачи линейного программирования с зависящими от параметра коэффициентами, сводимой к решению системы неравенств одного знака, которая в свою очередь сводится к одному неравенству. Этот метод позволяет получить оптимальное решение в виде функции от параметра, определяющего возможные изменения коэффициентов задачи.

Статья в формате PDF

845 KB

неравенства

линейное программирование

симплекс-метод

метод Жордана – Гаусса

целевая функция

экстремум

матрица

1. Гольштейн Е.Г., Юдин Д.Б. Новые направления в линейном программировании. – М.: Советское радио, 1966.

2. Кравчук С.П., Кравчук И.С., Швед Е.В. Экстремумы в системе линейных неравенств с двумя переменными. – СПб.: Современные аспекты экономики, 2010. – № 6 (154).

3. Кравчук С.П., Кравчук И.С., Татарников О.В., Швед Е.В. Метод неравенств в задачах линейного программирования. – М.: Фундаментальные исследования, 2014. –№ 3, часть 1.

4. Общий курс высшей математики для экономистов: учебник под ред. проф. В.И. Ермакова. – М.: ИНФРА-М, 2000.

5. Юдин Д.Б., Гольдштейн Е.Г. Линейное программирование. – М.: ФизМатГиз, 1963.

В работах [2, 3] предложен простой метод решения задач линейного программирования, основанный на последовательном исключении переменных в системе линейных неравенств. Важным преимуществом этого метода перед симплексным является возможность решения задач с параметрами, т.е. получение окончательного результата в виде функции от этих параметров. В данной работе рассматривается однопараметрическая задача линейного программирования с двумя неотрицательными переменными, в которой часть коэффициентов (или все) зависят от одного общего параметра. Экстремум целевой функции и опорное решение станут аналитически зависеть от этого параметра.

Найдём методом неравенств [2] решение следующей задачи:

Z = x₁ + 3x₂ → min;

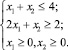(1)

Её легко решить графоаналитическим способом [4, 5]:

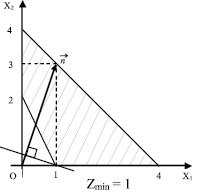
Рис. 1

Как видно из рис. 1, Zmin = 1 при x1 = 1, x2 = 0.

Это решение является частным для более общей задачи с переменными коэффициентами:

Z = (1 + C1)x1 + (3 + C2)x2 → min;

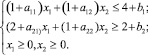(2)

Здесь буквенные величины задают отклонения от значений коэффициентов задачи (1). Условиям (2) соответствует система неравенств

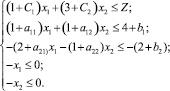(3)

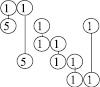
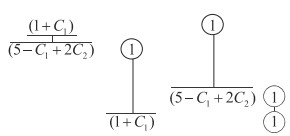
Начало таблицы решений выглядит так:

Таблица 1

Для дальнейшего решения требуется задать конкретный вид отклонений коэффициентов (3). Пусть параметр t меняется в пределах от 0 до 1:t ∈[0; 1].

Чтобы отклонения коэффициентов по абсолютной величине были невелики, будем отсчитывать их от среднего значения параметра t = 1/2. Все отклонения предполагаются линейными функциями, пропорциональными t – 1/2. Коэффициенты пропорциональности выберем, например, такими, чтобы максимальные отклонения не превышали 10 % от значений коэффициентов (2).

Отметим, что допущение малой изменчивости коэффициентов рассматриваемой задачи делается только с целью сохранения их знака при этих t, что сокращает трудоёмкость решения задачи. При произвольных законах изменения коэффициентов aik(t) и Cj(t) следует весь промежуток изменения параметра t разбить на ряд интервалов, в пределах которых знак этих коэффициентов остаётся неизменным. Это позволит правильно выбирать складываемые неравенства. В итоге процесс решения по сути не изменится, а только удлинится, т.к. придётся искать Zmax(t) на каждом из данных интервалов.

Случай переменных свободных членов

Проще всего задача (2) решается, когда C1 = C2 = 0; a11 = a12 = a21 = a22 = 0. Тогда табл. 1 принимает вид табл. 2.

Если предположить, что |b1| ≤ 0,4 и |b2| ≤ 0,2, то решением полученной системы неравенств будет Zmin = 1 + 0,5b2. При этом x1 = 1 + 0,5b2; x2 = 0. Если, например, положить

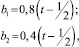(4)

то

Zmin(t) = 0,2t + 0,9;

x1 = 0,2t + 0,9; x2 = 0. (5)

Таблица 2

При этом

Zmin ∈[0,9; 1,1]; Zcp = Zmin(1/2) = 1;

x1 ∈[0,9; 1,1];

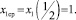
Случай переменных коэффициентов целевой функции и свободных членов

Пусть a11 = a12 = a21 = a22 = 0; |C1| ≤ 0,1; |C2| ≤ 0,3; |b1| ≤ 0,4; |b2| ≤ 0,2. Тогда табл. 1 станет выглядеть так:

Таблица 3

При рассматриваемой малости отклонений решение последней системы таково:

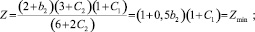
x1 = 1 + 0,5b2; x2 = 0.

Если принять

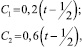(6)

а b1 и b2 взять из (4), то

Zmin(t) = (0,2t + 0,9)2;

x1 = 0,2t + 0,9; x2 = 0. (7)

При этом

Zmin ∈[0,81; 1,21]; Zcp = Zmin(1/2) = 1;

x1 ∈[0,9; 1,1];

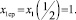
Случай всех переменных коэффициентов

Теперь в дополнение к (4), (6) примем

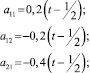
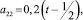(8)

так, что |a11| ≤ 0,1; |a12| ≤ 0,1; |a21| ≤ 0,2; |a22| ≤ 0,1.

Тогда из табл. 1, как и из табл. 2 и 3, можно найти

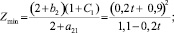(9)

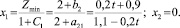
При этом

Zmin ∈[0,74; 1,34]; Zmin(1/2) = 1;

x1 ∈[0,82; 1,22]; x1(1/2) = 1.

Результаты (5), (6), (9) показывают, что не все переменные коэффициенты влияют на Zmin(t), x1(t), x2(t).

Для наглядности изобразим графики функций Zmin(t).

Из рис. 2 видно, что даже при небольших отклонениях коэффициентов задачи от их средних значений отклонение Zmin от среднего значения Zcp = 1 может быть немалым.

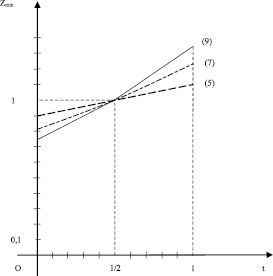
Рис. 2

Существует способ решения параметрических задач линейного программирования на основе симплекс-метода [1]. Однако этот способ непрост и довольно трудоёмок. В результате есть риск получить ошибочное решение. В качестве примера рассмотрим следующую задачу из [1].

Z = –x1 + 2x2 – 3x3 – x4 > MAX;

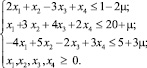(10)

Согласно [1],

(11)

При остальных ? Zmax не существует.

Решим (10) методом неравенств. Составляя таблицу, подобную табл. 1, и исключая все переменные, в итоге получим систему из 23-х неравенств вида

(12)

Для нахождения Zmax(μ) построим графики всех прямых, отвечающих правым частям неравенств для Z. Затем выберем среди них прямые с наименьшими ординатами. Они и составят график Zmax(μ) на рис. 3.

Этому графику соответствуют первые 5 неравенств (12):

(13)

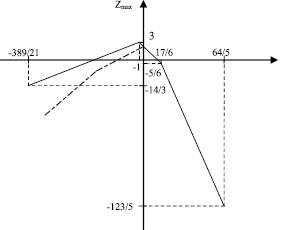
Рис. 3

На рис. 3 штрих-пунктиром нанесено и решение (11). Как видно, (11) и (13) отличаются при μ < 0, что свидетельствует о том, что решение, приведенное в [1], ошибочно.

Сравнение представленных методов решения задачи (10) позволяет сделать вывод, что метод неравенств является более простым и надежным по сравнению с симплекс-методом.

Рецензенты:

Титов В.А., д.э.н., профессор кафедры информационных технологий, ФГБОУ ВПО «Российский экономический университет имени Г.В. Плеханова», г. Москва;

Туганбаев А.А., д.ф.-м.н., профессор кафедры высшей математики, ФГБОУ ВПО «Национальный исследовательский университет «МЭИ», г. Москва.

Работа поступила в редакцию 23.09.2014. 

Библиографическая ссылка