Научный журнал

Фундаментальные исследования

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Наумова Н.А. 1 Данович Л.М. 1 Данович Ю.И. 1

---

1 ФГБОУ ВПО «Кубанский государственный технологический университет» Министерства образования и науки РФ

Проблема оптимального распределения транспортных потоков по улично-дорожной сети является очень актуальной, так как градостроительные особенности не позволяют постоянно расширять улично-дорожную сеть за счет введения ее новых элементов. Благодаря развитию вычислительной техники появилась возможность оперативно и эффективно координировать организацию движения автотранспортных средств по улично-дорожной сети. В работе приведен и обоснован метод решения важной практической задачи: определение изменений в распределении транспортных потоков по сети при введении в эксплуатацию новых потокообразующих элементов. Разработанный алгоритм базируется на авторской математической модели распределения транспортных потоков по сети, которая обеспечивает оперативный обмен данными между микро- и макромоделями. Алгоритм построен с учетом теории потокового равновесия и удовлетворяет первому принципу Вардропа. Разработанные алгоритмы реализованы в виде компьютерных программ в среде DELPHI 7.

Статья в формате PDF

1062 KB

транспортный поток

математическая модель

функция транспортных затрат

пара «источник – сток»

оптимальный маршрут

1. Домбровский А.Н., Наумова Н.А.Транспортные потоки на улично–дорожной сети городов: моделирование и управление : монография / Кубан. гос. технол. ун–т. – Краснодар : Издательский Дом – Юг, 2012. – 124 с.

2. Гасников А.В. и др. Введение в математическое моделирование транспортных потоков: учеб. пособие / Гасников А.В., Кленов С.Л., Нурминский Е.А., Холодов Я.А., Шамрай Н.Б. под ред. Гасникова А.В. – М.: МФТИ, 2010. – 362 с.

3. Наумова Н.А. Метод определения функции транспортных затрат в узловых точках сети.//Фундаментальные исследования. – 2013. – №8 (ч. 4), С. 853–857. 

4. Наумова Н.А. Метод определения функции транспортных затрат для узловой точки сети типа «нерегулируемое пересечение потоков требований». //Фундаментальные исследования.– 2013. – №10 (ч. 4). – С. 17–722 

5. Наумова Н.А., Данович Л.М., Данович Ю.И. Определение параметров распределения обобщенного закона Эрланга по экспериментальным данным при изучении транспортных потоков // Современные проблемы науки и образования. – 2013. – № 5. URL: http://www.science–education.ru/111–10045   

6. Семенов В.В. Математическое моделирование динамики транспортных потоков мегаполиса: обзорный реферат. – М., 2003. – 44 с.

7. Швецов В.И. Математическое моделирование транспортных потоков // Автоматика и телемеханика. – 2003. – №11. – С.3–46

Проблема эффективного использования улично-дорожной сети (УДС) населенных пунктов, несомненно, очень актуальна. В связи со значительным ростом числа владельцев личного автотранспорта, высокой мобильностью населения крупных городов транспортная сеть городов заметно перегружена. Градостроительные особенности не позволяют постоянно расширять улично-дорожную сеть за счет введения ее новых элементов. Следовательно, требуется грамотное управление транспортными потоками по уже существующей УДС. Несмотря на существование многочисленных математических моделей и методов, применяемых для анализа транспортных сетей [2,6,7], требуется постоянное их усовершенствование. Благодаря развитию вычислительной техники, появлению новых технических средств, позволяющих контролировать текущее состояние потоков на сети, появилась возможность оперативно и эффективно координировать организацию движения автотранспортных средств по УДС.

Авторами разработана математическая модель распределения транспортных потоков по улично-дорожной сети [1,3], в основу которой положена гипотеза о распределении интервалов по времени между автотранспортными средствами по полосам движения по обобщенному закону Эрланга. На базе этого выведена в явном аналитическом виде функция транспортных затрат как функция от параметров распределения потоков по всем направлениям движения в узловых точках сети [3,4]. Параметры распределения обобщенного закона Эрланга для каждого направления движения, в свою очередь, являются функциями от интенсивности транспортного потока [5].

Математические модели, применяемые для автоматизированного управления УДС, могут быть построены с применением различных математических теорий. Это может быть объектно-ориентированное программирование, рассматривающее отдельные физические объекты и взаимодействие между ними. При построении собственной модели авторы применяли теорию графов. Узловые точки (УТ) графа – пересечения транспортных потоков (перекрестки), дуги графа – отдельные полосы движения между соседними перекрестками. Поток на графе задан в виде функции плотности распределения интервалов по времени между автотранспортными средствами.

В данной работе приведен и обоснован метод решения следующей важной практической задачи: какие изменения в распределении транспортных потоков по сети повлечет за собой введение в эксплуатацию новых потокообразующих элементов. Использование в расчетах выведенной авторами функции транспортных затрат обеспечивает оперативный обмен данными между микро- и макромоделями. Транспортные затраты в узлах сети меняются при изменении схемы организации дорожного движения по сети в целом, а их пересчет происходит в ходе выполнения разработанных алгоритмов.

Метод расчета распределения интенсивностей транспортных потоков по полосам движения улично–дорожной сети исходя из матрицы корреспонденций при введении в эксплуатацию нескольких пар «источник–сток»

В основу разработанного алгоритма положен принцип транспортного (потокового) равновесия, удовлетворяющего первому принципу Вардропа, согласно которому каждый водитель выбирает путь с наименьшими транспортными расходами. Причем выбор отдельного водителя влияет на загрузку сети, а следовательно, влияет на выбор следующих пользователей для той же пары «источник – сток». В работе будем придерживаться обозначений, принятых в учебном пособии [2]:

i – общий объем пользователей, которые должны прибыть из пункта i в пункт j;

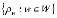– матрица корреспонденций;

х_p – величина потока, идущего по пути p∈P;

N_p – интенсивности движения по дугам маршрута p;

x = x_p:p∈P – вектор потоков по всем путям p∈P;

G_P – функция транспортных затрат на проезд по пути p;

y_e – величина потока по дуге e∈E;

y = y_e:e∈E – вектор, описывающий загрузку дуг сети;

,

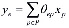где

;

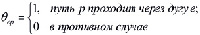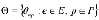– матрица инцидентности дуг и путей.

Пусть ω₁=(i₁,j₁), 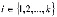– пары «источник – сток», вводимые в эксплуатацию. Будем считать заданной базу данных А₀, составленную в соответствии с требованиями нашей математической модели автотранспортной сети. Предвидятся изменения в распределении интенсивностей транспортных потоков, вызванные введением в эксплуатацию нескольких новых источников или стоков требований. Составлена матрица корреспонденций, отражающая предстоящие изменения.

Идея алгоритма состоит в следующем: определяются оптимальные маршруты между парами «источник – сток» при существующем распределении интенсивностей. Затем увеличивается по всем оптимальным маршрутам интенсивность на малую величину, и вновь выбирается оптимальный маршрут, отвечающий пользовательскому оптимуму. В данном случае функция транспортных затрат по маршруту не является монотонной относительно распределения интенсивностей по дугам данного маршрута.

Модуль 1 (определение «кратчайшего» пути между двумя вершинами).

Каждой дуге графа соответствует число 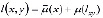– «длина» дуги; если вершины не соединены дугой, то l(x,y) = ∞.

В ходе выполнения алгоритма вычисляют величины d(x), равные кратчайшему пути из вершины s=z₀ в вершину х:

.

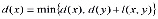В нашем случае l(x, y) – функция транспортных затрат G_P (x) ≡ G_P (x(Np) потока от источника i=x до стока j=y.

Необходимые для решения задачи данные будут храниться в двух массивах:

MPlus – данные об узловых точках, имеющих постоянные метки;

MMinus – данные об узловых точках, имеющих временные метки.

Каждый элемент массивов имеет следующую структуру:

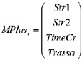и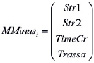

Str1 – магистраль, по которой совершалось движение до данной узловой точки;

Str2 – магистраль, пересекающая Str1;

TimeCr – время движения d(x) до данной узловой точки от начальной точки маршрута;

Trassa – перечень пройденных узловых точек.

1-й шаг. Задаем начало и конец маршрута. Узловую точку (УТ) – начало пути заносим в массив MPlus под номером n = 0 и в массив MMinus под номером 4n.

2-й шаг. Определяем все узловые точки, смежные с УТ № n, и заносим в массив MMinus данные о них под номерами (4n + 1), (4n + 2), (4n + 3).

Если вершины не являются смежными или движение в этом направлении запрещено, то l(x,y) = ∞.

3-й шаг. Вычисляем функцию транспортных затрат от УТ № n до всех смежных с ней, не занесенных в массив MPlus.

4-й шаг. Выбираем минимальный элемент в поле MMinus.TimeCr и заносим данные о соответствующей УТ в массив MPlus под номером (n+1). Из массива MMinus данные об этой УТ удаляем.

5-й шаг. Повторяем шаги 2 – 4 до тех пор, пока УТ № (n+1) в массиве MPlus не совпадет с концом маршрута. Если УТ № (n + 1) в массиве MPlus совпала с концом маршрута, то расчеты заканчиваем.

6-й шаг. Массив MPlus – список УТ, через которые пролегает кратчайший маршрут p0 между двумя данными точками сети.

При расчетах в качестве отдельного модуля (модуль 2) используется алгоритм определения оптимального маршрута для данной пары ω1 = (i1,j1) и предполагаемого увеличения интенсивности по дугам этого маршрута.

Модуль 2 (алгоритм определения оптимального маршрута для данной пары ω1 = (i1,j1) и предполагаемое увеличение интенсивности по дугам этого маршрута).

1-й шаг. Составляем оптимальный (по пользовательскому оптимуму) маршрут p0 между источником и стоком для отдельного требования; вычисляем среднее время t0 движения по маршруту (модуль 1).

2-й шаг. Определяем количество требований, которые должны воспользоваться данным маршрутом p0 в течение определенного времени (данные берем из матрицы корреспонденций).

3-й шаг. Определяем предполагаемое увеличение интенсивности по дугам ΔNe, связанное с данной парой «источник – сток»:

.

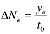Алгоритм определения базы данных распределения интенсивностей транспортных потоков по сети.

1-й шаг. Определяем оптимальный маршрут для каждой из пар ω₁=(i₁,j₁), 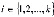«источник – сток» (модуль 2).

2-й шаг. Задаем точность ε и составляем новую базу данных А₀, в которой увеличение интенсивности по дугам каждого из маршрутов pei произведено на величину .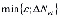

3-й шаг. Корректируем матрицу корреспонденций с учетом распределенных требований.

4-й шаг. Повторяем пункты 1 – 3 до тех пор, пока по маршрутам не будут распределены все требования (с точностью до ε).

В предлагаемом алгоритме учитывается тот факт, что каждый водитель выбирает путь с наименьшими транспортными расходами. При этом предполагается осведомленность водителей о текущем состоянии загруженности транспортной сети. Данное предположение не является «фантастическим» при современном уровне оснащенности водителей автотранспорта техническими средствами. Кроме того, при многократном повторении эксперимента система сходится к равновесному распределению потоков.

Заключение

Математическое моделирование является важным инструментом, позволяющим решать задачи оптимального управления транспортной сетью городов, прогнозировать изменения в уровне загрузки улично-дорожной сети, вызванные появлением новых «центров притяжения» клиентов. Выгодным отличием разработанной авторами модели от других существующих является тот факт, что транспортные затраты в узлах сети при введении изменений по организации движения на всей улично-дорожной сети пересчитываются в процессе работы алгоритма без привлечения новых исходных данных.

В настоящее время существуют различные системы автоматического управления дорожным движением (АСУДД). Предложенные в работе алгоритмы реализованы в виде компьютерных программ в среде DELPHI 7 и могут служить отдельным модулем в существующих АСУДД.

Работа выполнена при поддержке РФФИ и администрации Краснодарского края, проект р–юг–а–13–08–96502.

Рецензенты:

Атрощенко В.А., д.т.н., профессор, декан факультета компьютерных технологий ФГБОУ ВПО «Кубанский государственный технологический университет» Министерства образования и науки РФ, г. Краснодар;

Видовский Л.А., д.т.н., профессор, заведующий кафедрой вычислительной техники и автоматизированных систем управления ФГБОУ ВПО «Кубанский государственный технологический университет» Министерства образования и науки РФ, г. Краснодар.

Работа поступила в редакцию 10.06.2014.

Библиографическая ссылка