Обработка деталей на автоматизированном металлорежущем оборудовании должна осуществляться оптимальными режимами резания, при которых достигается наибольшая производительность и выполняются технологические требования к качеству обработанной поверхности, обеспечивается нормативная стойкость инструмента. Оптимальный режим резания определяется многими факторами: материалом заготовки и инструмента, геометрией режущей части инструмента, его стойкостью, требованиями к точности и шероховатости обработанной поверхности [5]. В станочных системах обработка деталей требуемой формы и размеров требует выполнения согласованных друг с другом рабочих движений и движении инструмента и заготовки. К рабочим движениям относят главное движение и движение подачи, которые, как правило, кинематически связаны друг с другом. Однако изменение сил резания в процессе резания обработки нарушает эту связь.
Рассматривается взаимодействие рабочих движений в координатно-сверлильном полуавтомате. Здесь главное движение при сверлении – вращение инструмента, движение подачи – поступательное движение пиноли с инструментом. Среди параметров режимов резания наибольшее влияние на качество обработки оказывает величина оборотной подачи инструмента [1, 5]. Поэтому качество обработки отверстия достигается стабильностью её величины Sоб(t). Это становится возможным, если при уменьшении скорости вращения инструмента синхронно уменьшается скорость подачи vп, обеспечиваемая приводом подачи станка. Возможности обеспечения кинематической жесткости каждого из рабочих движений в условиях применения гидропривода, как известно, ограничены [5]. Без учета упругих деформаций в кинематической цепи подачи инструмента величина подачи на оборот инструмента определяется
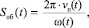 (1)
(1)
где vп(t) – скорость подачи инструмента, мм/c; ω(t) = 2πn(t) – скорости вращения инструмента, рад/c; n(t) – частота вращения инструмента, об/c–1.
При проектировании системы приводов рабочих движений координатно-сверлильного полуавтомата для повышения производительности и точности обработки отверстии использовали предлагаемый подход. Общий вид станка представлен на рис. 1.
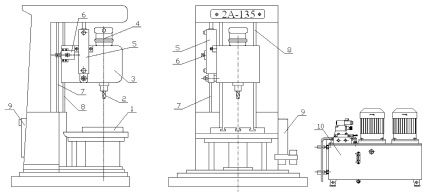
Рис. 1. Общий вид координатно-сверлильного полуавтомата: 1 – координатный стол; 2 – сверлильная головка; 3 – пиноль; 4 – гидромотор ГМ главного движения; 5 – гидроцилиндр ГЦ движения подачи; 6 – гидравлический датчик; 7 – зубчатая рейка; 8 – направляющие; 9 – блок управления; 10 – насосная установка
Принципиальная гидрокинематическая схема сверлильной головки станка представлена на рис. 2. Она определяет состав устройств, гидромеханические связи, основные параметры, характеризующие разветвленный привод.
При запуске включается электромагнит YA3 распределителя Р2, YA1 распределителя Р1 и YA5 распределителя Р3, насос подаёт жидкость в полость ГЦ и ГМ, проходит быстрый подвод системы подачи сверла. Система управления, построенная на основе программируемого логического контроллера (ПЛК) и мехатронного измерительного модуля, отслеживает перемещение ГЦ и при прохождении «координаты замедления» отключает электромагнит YA5 распределителя Р3. При этом обеспечиваетсяснижение скорости привода подачи сверла дорабочей подачи vп(t). Одновременно включается электромагнит YA1 распределителя Р1, включающего привод вращения инструмента.
Если в процессе резания крутящий момент на сверле увеличивается, уменьшается частота вращения сверла, в первый момент при сохранении подачи vп(t) инструмента возрастает его оборотная подача. В следующий момент увеличивается давление в напорной линии ГМ, что формирует управляющий сигнал Ру на клапан давления. Смещаясь.ю золотник клапана уменьшает его проточную часть, скорость перемещения гидроцилиндра уменьшается, при этом сохраняется величина оборотной подачи S0(t) и качество обработки отверстий.
После останова включается электромагнит YA4 распределителя Р2 и электромагнит YA2 распределителя Р1, перекрывая слив ГЦ и он останавливается. По команде ПЛК включаются электромагниты УА2 и УА5 распределителей Р2 и Р3. ГЦ возвращается в исходное положение.
Моделирование систем гидроприводов осложняется нестационарными гидромеханическими процессами. При формировании математической модели динамической системы предлагаемого гидропривода были приняты следующие допущения:
- Механическую подсистему описывает одномассовая динамическая система.
- Динамические процессы протекают в окрестности точки нагрузочной характеристики привода Рн = const, Qн = const.
- Рабочая жидкость сжимаемая, капельная, в каналах присутствует нерастворённый воздух. Сосредоточенный объём сжимаемой жидкости Qсж для удобства расчётов считаем присоединенным к рабочей полости гидродвигателя.
- Утечки в подвижных соединениях малы, они зависят главным образом от конструктивного исполнения и могут быть ограничены коэффициентом утечки kу.
- Сила вязкого трения в подвижных сопряжениях пропорциональна скорости. В реальных устройствах зависимость значительно сложнее. На силы трения, кроме скорости, оказывают влияние внешние факторы и состояние трущихся поверхностей.
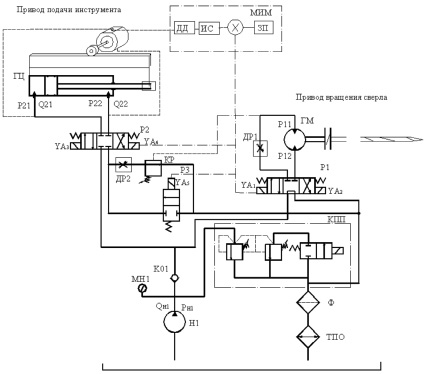
Рис. 2. Принципиальная гидрокинематическая схема координатно-сверлильного станка: ГЦ – гидроцилиндр; ГМ – гидромотор; МИМ – мехатронный измерительный модуль; КР – гидравлический управляющий клапан; Р1; Р2; Р3 – распределители; ДР1; ДР2 – дроссели; Н – насос; Ру – давление управления клапана; КПП – предохранительный клапан
Гидравлическая силовая подсистема дроссельного регулированного описывается уравнениями расходов, учитывающими условие неразрывности потока жидкости соответственно к напорной и сливной гидролиниям [3, 4].
Привод вращения инструмента описывают следующие уравнения:
1. Уравнение движения механической подсистемы:
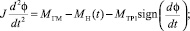 (2)
(2)
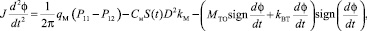
где J – приведенный момент инерции вращающихся масс привода, Н∙м4∙с–2; 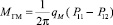 – крутящий момент гидромотора, Н∙м;
– крутящий момент гидромотора, Н∙м; 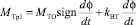 – момент трения, Н∙м;
– момент трения, Н∙м; 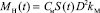 – крутящий момент резания, Н∙м.
– крутящий момент резания, Н∙м.
2. Уравнение расходов в напорной линии:
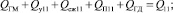 (3)
(3)
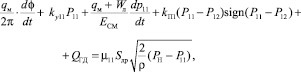
где 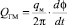 – расход ГМ, м3∙с–1; qгм – рабочие объемы ГМ, м3/об;
– расход ГМ, м3∙с–1; qгм – рабочие объемы ГМ, м3/об; 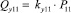 – расход, идущий на компенсацию утечек;
– расход, идущий на компенсацию утечек; 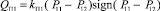 – расход, идущий на перетечки рабочей жидкости;
– расход, идущий на перетечки рабочей жидкости; 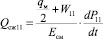 – расход, идущий на компенсацию деформируемого объема жидкости в полостях ГМ и подводящих каналах; Wij – объем гидролиний соответственно, м3;
– расход, идущий на компенсацию деформируемого объема жидкости в полостях ГМ и подводящих каналах; Wij – объем гидролиний соответственно, м3; 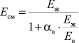 – модуль объемной упругости смеси жидкости и воздуха, Па; Eв, Eж – модули объемной упругости жидкости и воздуха; αв – содержание воздуха в жидкости; kу, kп– коэффициенты утечки и перетечки; Sдр – сечение проточной части дросселя, м2.
– модуль объемной упругости смеси жидкости и воздуха, Па; Eв, Eж – модули объемной упругости жидкости и воздуха; αв – содержание воздуха в жидкости; kу, kп– коэффициенты утечки и перетечки; Sдр – сечение проточной части дросселя, м2.
3. Уравнение расходов сливной линии:
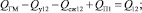 (4)
(4)
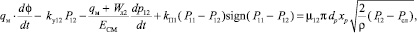
где 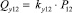 – расход, идущий на компенсацию утечек;
– расход, идущий на компенсацию утечек; 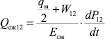 – расход, идущий на компенсацию деформируемого объема жидкости в полостях ГМ и подводящих каналах; dр – диаметр проточной части распределителя, м; хр – перемещение золотника распределителя, м.
– расход, идущий на компенсацию деформируемого объема жидкости в полостях ГМ и подводящих каналах; dр – диаметр проточной части распределителя, м; хр – перемещение золотника распределителя, м.
4. Уравнение гидравлического клапана привода подачи:
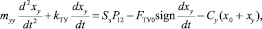 (5)
(5)
где mуу – приведенная масса перемещает золотник клапана и жидкости в гидролинии управления, кг; kту – коэффициент вязкого трения; су – жесткость пружины клапана, Н/м; Pу – давление управления клапана, мПа; SЗ – сечение золотника клапана, м2; Fту0 – сила сухого трения золотниковой пары клапана, Н.
Привод подачи инструмента описывается следующими уравнениями.
5. Уравнение движения гидроцилиндра с пинолем инструмента:
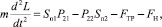 (6)
(6)
где L – перемещение поршня и пиноли, мм; m = mпч + mж – приведенная масса, кг; mпч – масса подвижных частей, кг; mж – масса жидкости, кг; 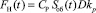 – осевая сила при сверлении, Н; СР, kР – коэффициенты зависят от условиях резания; Sn1, Sn2 – площади поршневой и штоковой полостей ГЦ, м2.
– осевая сила при сверлении, Н; СР, kР – коэффициенты зависят от условиях резания; Sn1, Sn2 – площади поршневой и штоковой полостей ГЦ, м2.
6. Уравнение расходов для напорной линии:
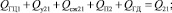 (7)
(7)
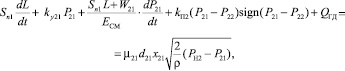
где QГД – расход гидравлического датчика, м3∙с–1.
7. Уравнение расходов для сливной линии:
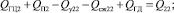 (8)
(8)
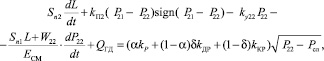
где 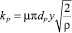 – коэффициенты проводимости проточной части потока распределителя; у – перемещение золотника распределителя; dр – диаметр золотника распределителя;
– коэффициенты проводимости проточной части потока распределителя; у – перемещение золотника распределителя; dр – диаметр золотника распределителя; 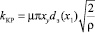 – коэффициенты проводимости проточной части потока клапана; ху – перемещение золотника клапана; dз – диаметр золотника клапана;
– коэффициенты проводимости проточной части потока клапана; ху – перемещение золотника клапана; dз – диаметр золотника клапана; 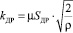 – коэффициенты проводимости проточной части потока дросселя; Sдр – сечение проводимости проточной части дроссели потока, м2; α = 0∨1 – Булев параметр, α = 1 при включении распределителя Р3; α = 0 при отключении распределителя Р3; δ = 0∨1 – Булев параметр, δ = 1 при xy(t) < xы; δ = 0 при xy(t) > x1.
– коэффициенты проводимости проточной части потока дросселя; Sдр – сечение проводимости проточной части дроссели потока, м2; α = 0∨1 – Булев параметр, α = 1 при включении распределителя Р3; α = 0 при отключении распределителя Р3; δ = 0∨1 – Булев параметр, δ = 1 при xy(t) < xы; δ = 0 при xy(t) > x1.
Исследование модели системы нелинейных дифференциальных уравнений (2)–(8) выполнено с использованием программной поддержки matlab численным методом Рунге–Кутта. Моделирование системы выполнено для типового рабочего цикл станочных систем: при включенном привода вращения инструмента и исходном положении привода подачи «стоп» после подачи команды на начало рабочего цикла осуществляются быстрый подвод инструмента к заготовке, рабочий ход, останов в конце рабочего хода с заданной точностью, реверсирование движения подачи и быстрый отвод сверлильной головки в исходное положение.
Результаты исследования динамической гидромеханической системы разветвленного гидропривода представлены на рис. 3 в виде осциллограмм изменения кинематических и силовых параметров при выполнении рабочего цикла. Введение в модель динамической системы разветвленного гидропривода, нестационарных гидромеханических характеристик давлений Pi, расходов в проточной части управляющих устройств, заметно усложняют [2].
На осциллограмме привода вращения сверла (рис. 3, а) видно, что скорость вращения ω(t) уменьшается при увеличении крутящего момента Мн (участок CD), это вызывает повышение давления в напорной полости ГМ, оно формирует сигнал управления Ру клапаном. Зависимость скорости вращения инструмента ω от крутящего момента Мн объясняется структурной неравномерностью скорости дроссельного гидропривода. Известно, что такие изменения возникают в электромеханических приводах.
Аналогичные изменения наблюдаются в приводе подачи инструмента. Увеличение усилия подачи Fн незначительно влияет на скорости подачи, подача изменяется на 5 % (v1, рис. 3, б). В этом случае существенно увеличивается величина оборотной подачи инструмента Sоб в сравнении с нормативной (рис. 3, в). Это приводит к нарушению режимов резания. В результате установлено, что при заданном изменении сил резания величина оборотной подачи (S1, рис. 3, в) при автономном приводе повышается в 2–2,3 раза. Во втором случае при зависимом приводе обеспечивается близко к нормативному значению оборотной подачи (S2, рис. 3, в) процесса обработки и требуемое качество обработки (рис. 3, в).
а 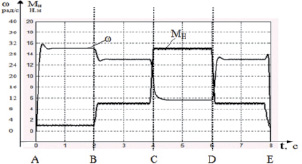
б 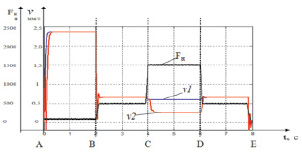
в 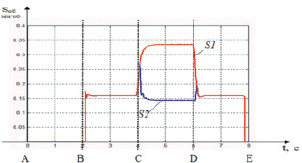
Рис. 3. Результаты моделирования динамической системы: а – привод вращения инструмента: ω – скорость вращения сверла, Мн – крутящий момент резания; б – привода подачи инструмент: Fн – усилие подачи, v1 – скорость подачи при автономном приводе, v1 – скорость подачи при зависимом приводе; в – величина оборотной подачи: S1 – при автономном приводе, S2 при зависимом приводе.
На основе аналитического описания динамики сверлильной головки и моделирования её рабочего цикла установлены основные параметры, влияющие на динамику привода, определены диапазоны их изменения, применительно к обработке отверстий. Установлено также удовлетворительное совпадение результатов вычислительного и натурного эксперимента при максимальном отклонении 12 % подтверждает достоверность полученных результатов и возможность их использования при проектировании реальных разветвленных гидроприводов.
Предложен, технически реализован, модельно описан принцип построения разветвленного гидропривода рабочих движений станочных систем с зависимым приводом подачи инструмента. На примере типового рабочего цикла сверлильной головки описана динамика поведения разветвленного гидропривода при изменяющихся нагрузках Мн, Fн. Анализ силовых и кинематических характеристик приводов позволил объяснить характер их изменения в реальном времени, оценить их качественно и количественно на примере сверлильной головки, а также предложить рекомендации, необходимые при создании аналогичной системы приводов.
Рецензенты:
Шошиашвили М.Э., д.т.н., профессор, заведующий кафедрой «Мехатроника и гидропневмоавтоматика», ФГБОУ ВПО «Южно-Российский государственный технический университет», г. Новочеркасск;
Заковоротный В.Л., д.т.н., профессор, заведующий кафедрой «Автоматизация производственных процессов», ФГБОУ ВПО «Донской государственный технический университет», г. Ростов-на-Дону.
Работа поступила в редакцию 23.08.2013.
Библиографическая ссылка
Сидоренко В.С., Ле Чунг Киен ДИНАМИКА РАЗВЕТВЛЕННОГО ГИДРОПРИВОДА РАБОЧИХ ДВИЖЕНИЙ СТАНОЧНЫХ СИСТЕМ // Фундаментальные исследования. – 2013. – № 10-3. – С. 509-505;URL: https://fundamental-research.ru/ru/article/view?id=32309 (дата обращения: 25.04.2024).



