1
Тахо-Годи А.З.
1
1 Донской государственный аграрный университет
В работе приводится информация о моделировании волн напряжений при взрывном воздействии в объекте угледобывающих предприятий с помощью численного метода Мусаева В.К. в перемещениях. Взрывное воздействие моделируется в виде дельта функции. Исследуемая расчетная область имеет 17112 узловых точек. Решается система уравнений из 68448 неизвестных. Показаны нормальные напряжения в характерных точках исследуемой области при взрывном воздействии. Задачи решаются с помощью численного моделирования двумерных плоских уравнений волновой теории упругости. Задача решается методом сквозного счета, без выделения разрывов. Основные соотношения метода конечных элементов в перемещениях получены с помощью принципа возможных перемещений. Для аппроксимации исследуемой области применяются треугольные и прямоугольные конечные элементы первого порядка. Получена явная двухслойная конечноэлементная схема.
моделирование
волны
характерная область
взрывное воздействие
объект
угледобывающее предприятие
численный метод
перемещение
нормальное напряжение
теория упругости
конечные элементы
алгоритм
комплекс программ
метод сквозного счета
1. Мусаев В.К. Решение задачи дифракции и распространения упругих волн методом конечных элементов // Строительная механика и расчет сооружений. – 1990. – № 4. – С. 74–78.
2. Мусаев В.К. Численное решение волновых задач теории упругости и пластичности // Вестник Российского университета дружбы народов. Серия «Прикладная математика и информатика». – 1997. – № 1. – С. 87–110.
3. Мусаев В.К. Численное моделирование напряженного состояния строительных конструкций при нестационарных динамических воздействиях // Архитектура оболочек и прочностной расчет тонкостенных строительных и машиностроительных конструкций сложной формы. Труды Международной научной конференции. – М.: РУДН, 2001. – С. 289–296.
4. Мусаев В.К. Численное решение некоторых задач безопасности жизнедеятельности с помощью метода конечных элементов // Вестник Российского университета дружбы народов. Серия проблемы комплексной безопасности. – 2005. – № 1. – С. 17–23.
5. Мусаев В.К. О разрушениях в сложных деформируемых телах, вызванных импульсными воздействиями // Вестник Российского университета дружбы народов. Серия «Проблемы комплексной безопасности». – 2006. – № 1. – С. 36–42.
6. Мусаев В.К. О некоторых возможностях математического моделирования и численного компьютерного эксперимента // Вестник Российского университета дружбы народов. Серия «Проблемы комплексной безопасности». – 2006. – № 1. – С. 81–86.
7. Достоверность результатов численного метода Мусаева В.К. в перемещениях при решении задачи об отражении упругих волн напряжений в виде дельта функции от свободной поверхности / А.З. Тахо-Годи, С.В. Ситник, В.В. Куранцов, А.И. Кормилицин, С.В. Акатьев // Техносферная безопасность, надежность, качество, энерго- и ресурсосбережение: Т38. материалы Международной научно-практической конференции. Выпуск XIII. Т. 2. – Ростов на/Д.: Ростовский государственный строительный университет, 2011. – С. 280–284.
8. Тахо-Годи А.З. О методе решения нестационарных волновых задач с помощью численного метода Мусаева В.К. в перемещениях // Безопасность и экология технологических процессов и производств: материалы Всероссийской научно-практической конференции. – Поселок Персиановский Ростовской области: Донской государственный аграрный университет, 2012. – С. 73–78.
9. Musayev V.K. Testing of stressed state in the structure-base system under non-stationary dynamic effects // Proceedings of the second International conference on recent advances in geotechnical earthquake engineering and soil dynamics. – Sent Louis: University of Missouri-Rolla, 1991. – Vol. 3. – P. 87–97.
10. Тахо-Годи А.З. Моделирования волновых напряжений при взрывном воздействии в объектах угледобывающих предприятий с помощью численного метода Мусаева В.К. в перемещениях // Безопасность и экология технологических процессов и производств: материалы Всероссийской научно-практической конференции. – Поселок Персиановский Ростовской области: Донской государственный аграрный университет, 2012. – С. 78–85.
Поставленная задача реализуется с помощью уравнений математической нестационарной динамической теории упругости.
Некоторые результаты рассматриваемого численного метода приведены в следующих работах [1–7].
Рассмотрим задачу о воздействии сосредоточенного взрывного воздействия (рис. 2) в объекте неглубокого заложения на окружающую среду (рис. 1).
В точке C приложено нормальное сосредоточенное воздействие σy, которое при 0 ≤ n ≤ 10 (n = t/Δt) изменяется линейно от 0 до P, а при 10 ≤ n ≤ 20 от P до 0 (P = σ0, σ0 = –0,1 МПа – 0,1 МПа (–1 кгс /см2)).
Граничные условия для контура AIHG при t > 0 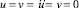 . Отраженные волны от контура AIHG не доходят до исследуемых точек при 0 ≤ n ≤ 150. Контур ABCDEFG свободен от нагрузок, кроме точки C, где приложено сосредоточенное взрывное воздействие.
. Отраженные волны от контура AIHG не доходят до исследуемых точек при 0 ≤ n ≤ 150. Контур ABCDEFG свободен от нагрузок, кроме точки C, где приложено сосредоточенное взрывное воздействие.
Расчеты проведены при следующих исходных данных:
H = Δx = Δy; Δt = 1,393∙10–6 с;
E = 3,15∙104 МПа (3,15∙105 кгс/см2);
ν = 0,2; ρ = 0,255∙104 кг/м3 (0,255∙10–5 кгс с2/см4);
Cp = 3587 м/с; Cs = 2269 м/с.
Исследуемая расчетная область имеет 17112 узловых точек. Решается система уравнений из 68448 неизвестных.
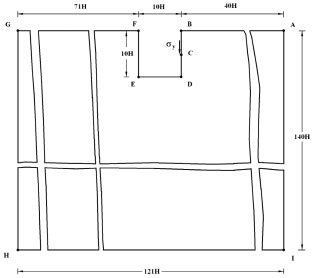
Рис. 1. Постановка задачи о сосредоточенном взрывном воздействии в объекте неглубокого заложения на окружающую среду
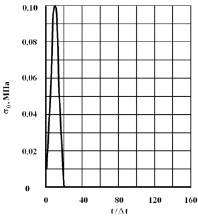
Рис. 2. Воздействие типа дельта функции
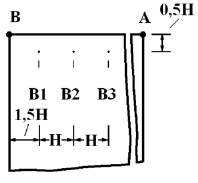
Рис. 3. Точки B1–B3, в которых приводятся упругие напряжения во времени
На рис. 4–6 показано изменение упругого нормального напряжения 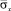 (
(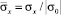 ) во времени n в точках B1–B3 (см. рис. 3), находящихся около свободной поверхности упругой полуплоскости.
) во времени n в точках B1–B3 (см. рис. 3), находящихся около свободной поверхности упругой полуплоскости.
Растягивающее упругое нормальное напряжение 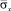 от точки B1 до точки В3 изменяется от значения
от точки B1 до точки В3 изменяется от значения 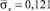 до значения
до значения 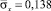 .
.
Сжимающее упругое напряжение 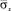 от точки B1 до точки В3 изменяется от значения
от точки B1 до точки В3 изменяется от значения 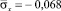 до значения
до значения  .
.
На основании проведенных исследований можно сделать следующие выводы:
1. Решена задача о сосредоточенном взрывном воздействии в объекте неглубокого заложения на окружающую среду. Взрывное воздействие моделируется в виде дельта функции. Исследуемая расчетная область имеет 17112 узловых точек. Решается система уравнений из 68448 неизвестных. Получены напряжения в характерных точках на поверхности упругой полуплоскости около объекта неглубокого заложения. Растягивающее упругое нормальное напряжение 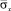 имеет следующее максимальное значение:
имеет следующее максимальное значение: 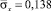 . Сжимающее упругое нормальное напряжение
. Сжимающее упругое нормальное напряжение 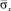 имеет следующее максимальное значение:
имеет следующее максимальное значение:  .
.
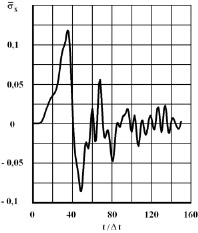
Рис. 4. Изменение упругого нормального напряжения во времени t/Δt в точке B1
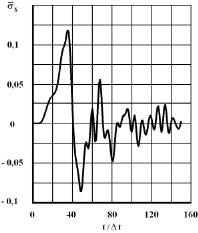
Рис. 5. Изменение упругого нормального напряжения во времени t/Δt в точке B2B2
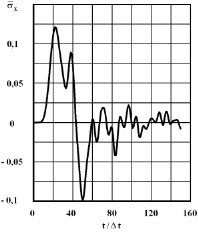
Рис. 6. Изменение упругого нормального напряжения во времени t/Δt в точке B3B3
2. Полученные результаты можно оценить как первое приближение о решении сложной комплексной задачи с помощью численного метода Мусаева В.К. для оценки напряженного состояния объектов угледобывающих предприятий при взрывных воздействиях.
Автор выражают благодарность Мусаеву В.К. за внимание к работе.
Рецензенты:
Мусаев В.К. Оглы, д.т.н., профессор, директор научно-производственной фирмы «Интерсейм», г. Пушкино;
Шаршак В.К., д.т.н., профессор кафедры «Механика, машины и оборудование пищевых производств» Донского государственного аграрного университета, г. Новочеркасск.
Работа поступила в редакцию 18.10.2012.
Библиографическая ссылка
Тахо-Годи А.З. ОПРЕДЕЛЕНИЕ НЕСТАЦИОНАРНЫХ НОРМАЛЬНЫХ ВОЛН НАПРЯЖЕНИЙ ПРИ ВЗРЫВНОМ ВОЗДЕЙСТВИИ В ОБЪЕКТЕ УГЛЕДОБЫВАЮЩИХ ПРЕДПРИЯТИЙ С ПОМОЩЬЮ ЧИСЛЕННОГО МЕТОДА МУСАЕВА В.К. В ПЕРЕМЕЩЕНИЯХ // Фундаментальные исследования. – 2012. – № 11-4.
– С. 956-959;
URL: https://fundamental-research.ru/ru/article/view?id=30691 (дата обращения: 17.04.2024).
Предлагаем вашему вниманию журналы, издающиеся в издательстве «Академия Естествознания»
(Высокий импакт-фактор РИНЦ, тематика журналов охватывает все научные направления)
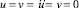 . Отраженные волны от контура AIHG не доходят до исследуемых точек при 0 ≤ n ≤ 150. Контур ABCDEFG свободен от нагрузок, кроме точки C, где приложено сосредоточенное взрывное воздействие.
. Отраженные волны от контура AIHG не доходят до исследуемых точек при 0 ≤ n ≤ 150. Контур ABCDEFG свободен от нагрузок, кроме точки C, где приложено сосредоточенное взрывное воздействие.



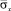 (
(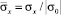 ) во времени n в точках B1–B3 (см. рис. 3), находящихся около свободной поверхности упругой полуплоскости.
) во времени n в точках B1–B3 (см. рис. 3), находящихся около свободной поверхности упругой полуплоскости.
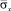 от точки B1 до точки В3 изменяется от значения
от точки B1 до точки В3 изменяется от значения 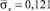 до значения
до значения 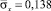 .
.
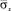 от точки B1 до точки В3 изменяется от значения
от точки B1 до точки В3 изменяется от значения 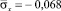 до значения
до значения  .
.
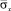 имеет следующее максимальное значение:
имеет следующее максимальное значение: 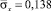 . Сжимающее упругое нормальное напряжение
. Сжимающее упругое нормальное напряжение 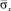 имеет следующее максимальное значение:
имеет следующее максимальное значение:  .
.






