Авторы [1] исследовали механизм распространения межфазных (внутригаллерейных) слоев в нанокомпозитах на основе эпоксиполимера, наполненных слоистым наполнителем, и предположили связь свойств нанокомпозитов со структурой указанных слоев. В настоящем сообщении в рамках фрактальной модели формирования межфазных слоев будет предложен молекулярный механизм их образования и количественно описано их влияние на степень усиления нанокомпозитов.
Использованы данные работы [1] для нанокомпозитов на основе эпоксиполимера, наполненного монтмориллонитом с содержанием 2,5, 10 и 15 вес. %. В качестве эпоксидного мономера использован 3,4-эпоксициклогексаметил-3,4-эпоксициклогексан карбоксилат, в качестве сшивающего агента - гексагидро-4-метилфталевый ангидрид (ГГМФА) при мольном соотношении эпоксидных групп к ГГМФА 1,0:0,87. Подробности получения нанокомпозитов изложены в работе [1]. Степень усиления нанокомпозитов Ек/Ем (где Ек и Ем - модули упругости нанокомпозита и матричного полимера, соответственно) оценивалась при температуре 313 К. Расстояние между пластинами монтмориллонита d001 получено с помощью широкоугловой рентгенодифрактометрии [1].
Степень усиления полимерных композитов может быть выражена отношением Ек/Ем и в рамках теории перколяции для нанокомпозитов она определяется следующим образом [2]:
![]() , (1)
, (1)
где φн и φмф - относительные доли наполнителя и межфазных слоев, соответственно.
Используя экспериментальные значения Ек, Ем и φн [1], можно рассчитать величины φмф согласно уравнению (1). Затем можно определить толщину межфазного слоя lмф из уравнения [2]:
![]() . (2)
. (2)
Построение графика lмф как функции расстояния между пластинами (интервала) d001 показало, что между указанными параметрами существует линейная корреляция, выражаемая следующим образом:
![]() . (3)
. (3)
Иначе говоря, из уравнения (3) следует, что все пространство между пластинами монтмориллонита (внутригаллерейное пространство) представляет собой межфазные слои. Нетрудно видеть, что такая трактовка позволяет прогнозировать степень усиления полимерных нанокомпозитов по уровню интеркаляции слоистого наполнителя, т.е., по величине d001. Согласно этой методике, по экспериментально определенным значениям d001 определяется lмф (уравнение (3)), затем φмф согласно уравнению (2) и далее теоретическая степень усиления (Ек/Ем)Т по уравнению (1). Это правило справедливо не только для сшитых матриц нанокомпозитов. Так, авторы [3] получили линейную зависимость Ек(d001) для нанокомпозитов на основе поликарбоната (ПК), наполненных монтмориллонитом, что подтверждает корректность предложенной модели. Более того, получено количественное соответствие предложенного метода прогнозирования и экспериментальных величин (Ек/Ем)Э для нанокомпозитов на основе ПК. Так, для d001=1 нм расчет дает (Ек/Ем)Т=1,183, а (Ек/Ем)Э=1,223 и для d001=3 нм (Ек/Ем)Т=1,596, (Ек/Ем)Э=1,479, т.е., в обоих случаях расхождение меньше 8 %, что сравнимо с погрешностью эксперимента.
Согласно определению, межфазным слоем является область полимерной матрицы, прилегающая к поверхности частицы наполнителя, и имеющая структуру, отличающуюся от структуры объемной полимерной матрицы. Поэтому возникает вопрос о природе отличия структуры этих двух компонент нанокомпозита. Авторы [1] предположили, что отличие состоит в пластификации межфазных слоев молекулами поверхностно-активного вещества (модификатора). В настоящем сообщении будет предложена другая трактовка, основанная на фрактальной природе микрогелей, которые для сшитых полимеров являются аналогом макромолекулярного клубка. Формирование микрогелей в пространстве, ограниченном пластинами монтмориллонита, будет изменять их структуру, характеризуемую фрактальной размерностью Df, и этот эффект ожидается тем сильнее, чем меньше d001. Теория фракталов в ограниченных геометриях дана в работе [4]. Минимальный размер поры (или галереи между пластинами монтмориллонита) D0, через которую макромолекулярный клубок или микрогель может проходить без изменения своей формы, дается уравнением [4]:
![]() , (4)
, (4)
где а - размер мономера, N - степень полимеризации, Df - фрактальная размерность микрогеля.
Оценим величину D0 при следующих условиях: а=0,6 нм, N=100 и Df=2,5. Тогда D0=19 нм. Следовательно, при любом d001<D0 микрогель будет изменять свою форму и, соответственно, структуру, характеризуемую величиной Df. Для наибольшей и наименьшей величин d001, полученных в работе [1] (13 и 6,3 нм, соответственно) оценки согласно (4) при а=const и N=const дают Df=2,334 и 2,020, соответственно.
Следовательно, первоначально сферический микрогель внутри галереи преобразуется в эллипсоид вращения, сплющенный тем более, чем меньше d001. Вариация Df приводит к изменению статистической гибкости полимерной цепи, характеризуемой характеристическим отношением C¥, согласно уравнению:
![]() , (5)
, (5)
где d - размерность евклидова пространства, в котором рассматривается фрактал (очевидно, в нашем случае d=3).
Изменение Df и С∞ приводит к вариации степени локального порядка, характеризуемой относительной долей областей этого порядка (кластеров) φкл согласно уравнению:
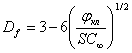 , (6)
, (6)
где S - площадь поперечного сечения макромолекулы (S=const).
Из уравнения (6) следует рост φкл по мере снижения Df, т.е., структура становится более плотноупакованной. Эти структурные изменения определяют различие объемной полимерной матрицы и межфазных слоев.
СПИСОК ЛИТЕРАТУРЫ
- Chen J.S., Poliks M.D., Ober C.K., Zhang Y., Wiesner U., Giannelis E. //Polymer. - 2002. - V. 43, № 19. - P. 4895.
- Козлов Г.В., Маламатов А.Х., Антипов Е.М., Яновский Ю.Г. //Механика композиционных материалов и констврукций. - 2006. - Т. 12, № 1. - С. 114.
- Yoon P.J., Hunter D.L., Paul D.R. //Polymer. - 2003. - V. 44, № 21. - P. 5323.
- Vilgis T.A., Haronska P., Benhamou M. //J. Phys. II. France. - 1994. - V. 4, № 12. - P. 2187.



