Essentially important desirable property of adaptive methods of synthesis of control algorithms is robustness, which, in this case, is understand as tolerance of results to changes of conditions of measuring. Robustness of algorithms is achieved by means of indemnification of disturbances to which influence the object of control is exposed. In the present paper the synthesis algorithm of robust control for nonlinear non-stationary systems with compensation of influence of disturbances and noises is offered by parametrical adaptation of a regulator and restoration of the current condition on previous.
Assume, that the mathematical model of functioning system is described by the system of nonlinear non-stationary difference equations of a kind [1]:
(1)
where x(k) - the m-dimensional vector, which components define a state of the system in a step k; u(k) - m-dimensional vector of control influences; 
- the matrix of parameters of object of control with (nxn) dimension, 
- the matrix of influence of control with (nxm) dimension; x0 - the initial condition of the system at the moment of time t0; (t0, N) - the period of simulation; the step k corresponds to the moment of time 
- the period of quantization of a signal on time.
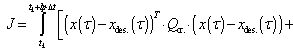
The cost function is 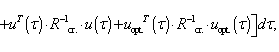[2]:
(2)
where 
- sliding interval of optimization of predicting model of a kind:
In (2) 
- nonnegative matrix (n x n), а 
- positive matrix (m x m); xdes - desired state of the system; uopt. - optimum control, minimizing (2).
The length of the interval of optimization is calculated as follows [3]:
where ceil - the function of a rounding off of value up to an integer, norme - Euclid´s norm of a matrix; matrixes 
are calculated on a condition 
, found in result of "run" of predicting model for one step.
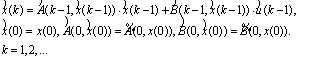
We synthesize the controller providing tracking property of the system to the set condition and a minimum of cost function (2). Control K(k) is defined as:
where 
- the solution of system of difference equations in back time:
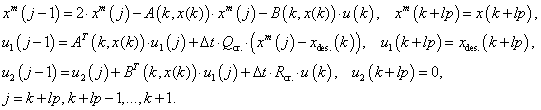
Control value u(k) is searched as [4]:
where 
, 
- elements of matrixes 
accordingly.
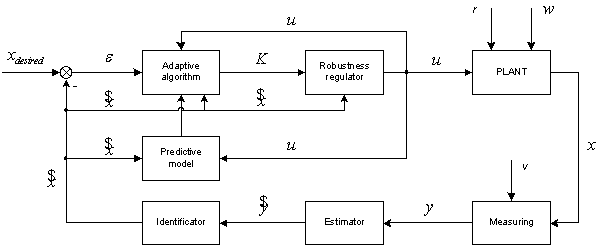
Fig. 1. The Structure of an adaptive control system with robust regulator
On the fig. 1: r - not measured disturbances, influencing in the uncontrollable way on properties of object of control, i.e. on matrixes 
and 
of parameters of the system; w and v - randomize values, described as "mean-zero Gaussian noises".
The measuring channel is described by the equation:
where C - the matrix of measuring channel with (m x n)dimension.
The estimating of states of system and identification of its not measured parameters is realized by two in parallel working discrete Kalman´s filters.
Let´s present the equation (1) as:
where 
- n-dimensional vector, which includes non measured parameters.
Thus the measuring channel becomes:
The recursive algorithm for an estimation of states [2]:
Here Q, R - covariance matrixes for noises w and v accordingly, I - identify matrix; 
- is the estimate of x(k) given past measurements up to y(k - 1); 
is the updated estimate based on the last measurement y(k).
In the block kind discrete Kalman´s filter:
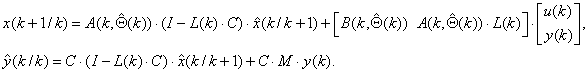
Identification of parameters we will realize by following Kalman´s filter:
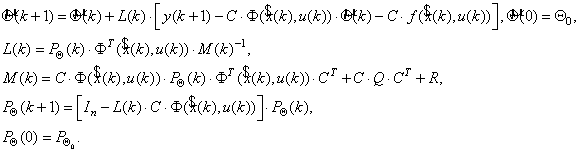
The developed algorithm has been used in the control system for controlling a speed of turning of blades of a propeller of a vessel. At sufficiently great speed of the ship turning of blades of a propeller with rated speed (1.8 degrees per second) result in sharp increase of torque in the diesel engine that is inadmissible as a safety matter. For functioning system with the set requirements (rates a torque of the engine is in allowable limits) also is necessary to take into account external disturbances (for example, influence of waves). Transients on a angle of turn of blades are performed on fig. 2.
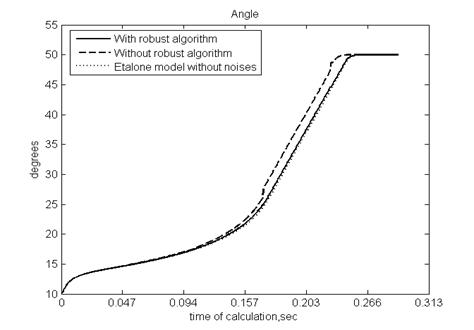
Fig. 2. The result of simulation (angle of turning of propeller blades)
Estimations of a root-mean-square deviation of transients from a standard (etalon) trajectory are counted: 2.5353 for algorithm without robust regulator and 0.4174 - with it. According to the results, it is possible to conclude efficiency of the desired algorithm.
Still recently rough systems keeping the characteristics at deviations of parameters from settlement values were projected, as a rule, "to the touch" by simple selection of parameters at modeling as regular procedures of designing were not in most cases.
In the modern control theory more and more attention is given to sensitivity of algorithms for disturbances.
REFERENCE
- Su D., Meyer A. Modern theory of automatic control and its application. - Moscow: Mechanical engineering, 1972. - 544 pp.
- Reshetnikova G.N. Adaptive control of linear discrete stochastic systems by criterion of the generalized work //Proceedings of the Academy of Sciences the USSR. Tech. Cybernetics. - 1989. - №3, 11 pp.
- Bukreev V.G., Krasnov I.Yu. Algorithm of optimum control of non-stationary electromechanical objects //Materials of IV All-Russian scient.-tech. conf. (MAMI-2003) «Measurements, automation and modeling in the industry and scientific researches». - Biisk, 2003. - p. 8-11.
- Granichin O.N., Polyak B.T. Randomized algorithms of estimating and optimization at almost arbitrary noises. - Moscow: The Science, 2003. - 291 pp.