Производственный процесс – упорядоченная, регулярная последовательность взаимосвязанных технологических процедур, которая превращает исходные ресурсы в конечные продукты [1]. До середины 1980-х гг. процесс производства представлялся вторичным по отношению к конечному продукту, т.е. на предприятиях существовал продуктовый подход. В настоящее время любой производственный процесс рассматривается как основное средство получения прибыли и повышения конкурентоспособности.
При процессном подходе производство конечного продукта представляется сетью связанных между собой технологических стадий, в ходе которых осуществляется преобразование входных ресурсов в выходную продукцию; при этом стабильный, точно исполняемый, высококачественный технологический процесс наиболее эффективно и с минимальными затратами обеспечивает получение продукции запланированного качества. С научной точки зрения технологический процесс представляется как последовательная закономерная смена некоторых явлений, состояний, а также как комплекс последовательных этапов для достижения результата. При этом выделяются два главных признака: динамизм, отождествляемый с постоянной сменой состояний, и цель функционирования, или по-другому цель управления.
Цели исследования
Если рассматривать последовательность технологических стадий как кибернетическую систему, то ее можно представить в виде схемы некоторого многомерного объекта, на входе у которого векторная переменная Z с компонентами z1, …, zk, объединяющая нерегулируемые характеристики объекта, векторная переменная X(t) с компонентами х1(t), …, хn(t), включающая условия протекания производственного процесса, а также вектор случайных переменных. Выходные данные описываются вектором Y(t) = y1(t), …, ym(t), представленным показателями качества получаемого продукта. Таким образом, систему управления в общем виде можно рассматривать как систему преобразования случайных функций X(t) в случайные функции Y(t) [2]. Для того чтобы производственный процесс, включая технологический, был управляемым, необходимо определить для него входные контролируемые и изменяемые воздействия, установить детерминированные или вероятностные зависимости между входными воздействиями и выходными показателями выпускаемой продукции, разработать способы автоматического измерения входных воздействий к выходам параметров, создать методы управления. Вышеперечисленные условия представляют собой непростую комплексную задачу, в которой ключевой является проблема синтеза математической модели управления. В настоящее время имеется широкий выбор методов решения задачи управления качеством многошаговых процессов, но большинство из них являются детерминированными и не учитывают стохастический характер технологических производств. Исходя из этого, представляется перспективным использование вероятностного подхода к оценке качества производственных стадий [3].
Предмет исследования
Примером рассматриваемого технологического процесса послужила организация хлебопекарного производства (рис. 1, 2). Для описания процессов, протекающих в данной предметной области, использовались диаграммы IDEF0 и IDEF3 [1].
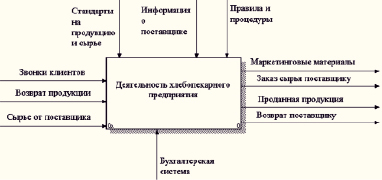
Рис. 1. Контекстная диаграмма модели деятельности хлебопекарного предприятия
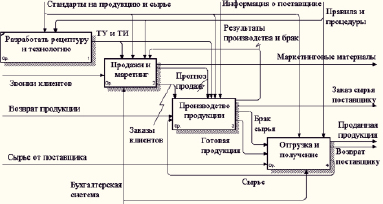
Рис. 2. Диаграмма декомпозиции А0 модели деятельности
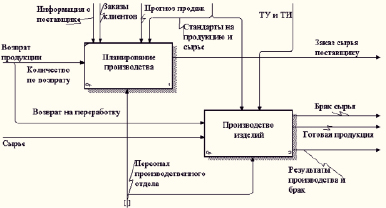
Рис. 3. Диаграмма А3 «Производство продукции»
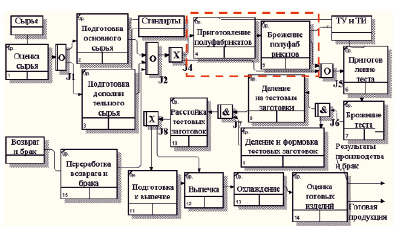
Рис. 4. IDEF3-диаграмма «Производство изделий»
Для понимания функционирования всей системы была выполнена декомпозиция блока «Производство продукции» (рис. 3): «Планирование производства»; «Производство изделий».
Особый упор при анализе и построении сделан на декомпозиции диаграммы А3 «Производство изделий», так как именно здесь перечислены основные технологические стадии хлебопекарного производства и их взаимосвязь (диаграмма А3.2.1) (рис. 4) [4]. Данная диаграмма представлена в виде IDEF3-модели.
Каждая из стадий, представленных на рис. 4, имеет некоторую вероятность качественного завершения. Однако если в случае неудовлетворительного выполнения операций по подготовке основного и дополнительного сырья, переработки и возврата брака, оценке готовых изделий, сырье и продукция дальнейшим производственным действиям не подвергается, другими словами, идет возврат, то при некачественном выполнении стадий по приготовлению полуфабрикатов, теста, расстойки тестовых заготовок и их выпечке, выход не отбраковывается, а подлежит дальнейшей переработке согласно технологическим инструкциям на данный вид изделия [5]. Исходя из этого, требуется проводить ряд мероприятий с целью улучшения качественного выполнения перечисленных операций.
Постановка задачи и способы ее решения
С целью оценки качества многошагового технологического процесса была выбрана концепция вероятностного управления, основанная на способе повышения вероятности качественного выполнения всего процесса за счет проведения некоторых мероприятий, обладающих минимальной стоимостью [6]; при этом рассматривался частный случай последовательно зависимых операций S1 – «приготовление полуфабрикатов» и S2 – «брожение полуфабрикатов» (рис. 4, выделение).
Для каждой i-й операции определялся набор ni мероприятий Mi1, Mi2,…, 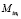 , проведение каждого из которых повышает вероятность качественного завершения операции
, проведение каждого из которых повышает вероятность качественного завершения операции 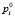 на некоторое значение
на некоторое значение 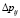 ,
, 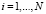 ,
, 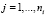 .. с минимальной суммарной стоимостью, который обеспечивает требуемый уровень качества проектирования. Причем одно мероприятие оказывает влияние только на одну операцию и не зависит от
.. с минимальной суммарной стоимостью, который обеспечивает требуемый уровень качества проектирования. Причем одно мероприятие оказывает влияние только на одну операцию и не зависит от 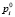 . А также стадии процесса являются независимыми в совокупности [7].
. А также стадии процесса являются независимыми в совокупности [7].
Тогда как для многих производств характерна последовательная взаимосвязь стадий. Поэтому рассмотренную модель неправомерно применять для таких процессов и требуется разработка модели, учитывающей поточность и зависимость производственных стадий.
Пусть имеется несколько последовательных стадий производства S1, S2,…, SN.
Будем считать, что вероятность качественного завершения i-й стадии зависит от того, как завершилась предыдущая (i – 1)-я стадия, для всех или для некоторых 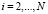 .
.
Тогда вероятность качественного завершения всех N стадий процесса, pкон, будет равна
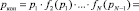
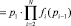 . (1)
. (1)
А для всех функций fi(p) справедливо соотношение:
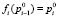 , (2)
, (2)
где 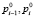 – соответственно начальные вероятности качественного завершения (i – 1)-й и i-й стадий.
– соответственно начальные вероятности качественного завершения (i – 1)-й и i-й стадий.
Были сделаны следующие предположения:
1) известны начальные значения вероятностей качественного завершения стадий (i – 1) и i;
2) для каждой стадии проводился набор мероприятий М;
3) одно мероприятие оказывает влияние только на одну стадию и не зависит от начальной вероятности;
4) каждое мероприятие увеличивает начальную вероятность на Δр и имеет стоимость с;
5) стоимость мероприятий не зависит от начального значения вероятностей.
Таким образом, для каждой стадии задаются ni-мерные вектор увеличения вероятностей 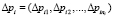 и вектор стоимостей
и вектор стоимостей 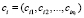 .
.
Введем для i-й стадии вектор 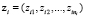 ,
, 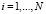 , каждая компонента которого может принимать значение 0 или 1.
, каждая компонента которого может принимать значение 0 или 1.
 (3)
(3)
Задача заключается в определении набора мероприятий с минимальной суммарной стоимостью, который обеспечивает достаточный уровень pпред вероятности качественного завершения всего производственного процесса.
Таким образом, получили следующую математическую модель оптимизационной задачи для многоэтапного процесса с последовательно зависимыми стадиями:
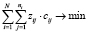 , (4)
, (4)
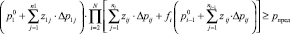 , (5)
, (5)
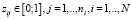 . (6)
. (6)
где N – число стадий процесса; ni – число проводимых мероприятий; zij – вектор, каждая компонента которого может принимать значение 0 или 1; cij – стоимость проводимого мероприятия; 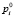 – исходная вероятность качественного завершения i-ой стадии; Δрij – значение, соответствующее увеличению исходной вероятности i-ой стадии при проведении j-го мероприятия; рпред – достаточный уровень вероятности всего многостадийного процесса.
– исходная вероятность качественного завершения i-ой стадии; Δрij – значение, соответствующее увеличению исходной вероятности i-ой стадии при проведении j-го мероприятия; рпред – достаточный уровень вероятности всего многостадийного процесса.
Для решения поставленной задачи (4)–(6) предлагалось использовать два способа: метод полного перебора и метод «ветвей и границ» [8]. Первый способ применим только при небольшом числе вариантов, получаемых при малом количестве проводимых мероприятий и стадий процесса. Второй способ позволяет уменьшить число итераций на каждом шаге вследствие выбора обобщенного мероприятия, которое увеличивает конечную вероятность качественного завершения процесса выше некоторой предельной величины рпред, а также обладает наименьшей суммарной стоимостью. Исходя из вышесказанного, при решении задачи использовался второй из указанных методов, при этом дерево решений имело 20 узлов, тогда как при полном переборе число узлов составляло 64.
Полученным решением является проведение для стадии S1 набора мероприятий М1 и М3, что позволяет увеличивать текущую вероятность качественного завершения стадии с 0,75 до 0,93; для стадии S2 – мероприятия М1 и М2, позволяющие повысить значение с 0,68 до 0,93. При этом вероятность всего процесса – 0,9114, общая стоимость проводимых мероприятий собщ составляет 37.
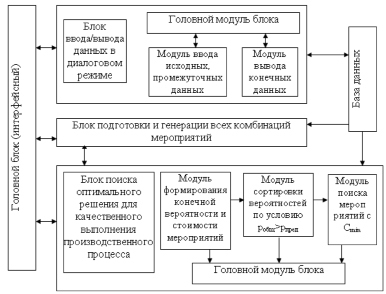
Рис. 5. Структура программного продукта «Информационная система управления качеством многошаговых вероятностных процессов»
Предлагаемая модель и алгоритмы реализованы в виде программного продукта оценки качества многошагового технологического процесса, позволяющего с использованием полученных теоретических результатов оптимально выбирать мероприятия влияния на стадии процесса. Функциональная структура программного комплекса представлена на рис. 5.
Выводы
Таким образом, на основе разработанных математической модели и алгоритмов, позволяющих осуществлять выбор мероприятий, направленных на повышение исходной вероятности качественного завершения процесса выше выбранного порогового значения, создана информационная система оценки качества многошагового технологического процесса, позволяющая с использованием полученных теоретических результатов оптимально выбирать мероприятия влияния на стадии процесса.



