Цель исследования
В последние два десятилетия для фильтрации дискретных сигналов часто используются алгоритмы, основанные на представлении фильтруемого сигнала в базисе вейвлет-функций [1–3]. Такие алгоритмы вейвлет-фильтрации включают три этапа:
- вычисление прямого дискретного вейвлет-преобразования (нахождение коэффициентов разложения в базисе вейвлет-функций зашумленных значений сигнала);
- обработка вычисленных «зашумленных» коэффициентов разложения;
- вычисление обратного дискретного вейвлет-преобразования от обработанных коэффициентов разложения (нахождение «отфильтрованных» значений сигнала) [4].
Очевидно, что качество фильтрации зашумленного сигнала определяется алгоритмами обработки, используемыми на втором этапе. Часто в качестве таких алгоритмов выступают так называемые пороговые алгоритмы: коэффициент разложения меньший по абсолютной величине некоторой пороговой величины полагается равным нулю, в противном случае такой коэффициент сохраняется или подвергается некоторому (в общем случае нелинейному) преобразованию (в зарубежной литературе такая обработка получила название thresholding [1]). Такой пороговый характер обработки приводит к появлению в отфильтрованном сигнале так называемых артефактов, т.е. новых составляющих (в большинстве случаев это осцилляции), которых не было в незашумлённом («точном») сигнале, что существенно ухудшает качество фильтрации.
Целью данной работы является разработка метода, позволяющего устранить эти артефакты. Предлагается метод, основанный на постобработке результата вейвлет-фильтрации пространственным алгоритмом фильтрации и существенно уменьшающий величину артефактов.
Пороговые алгоритмы и артефакты вейвлет-фильтрации сигналов
Алгоритмы вейвлет-фильтрации используют многомасштабное представление функции f(x) в базисе вейвлет-функций, которое имеет вид [1, 4, 5]:
.
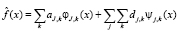Функции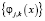 
называют масштабирующими (или отцовскими), а функции 
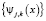– вейвлет-функциями (или материнскими). Коэффициенты разложения aj,k называют аппроксимирующими, dj,k – детализирующими, и они определяются выражениями:
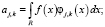
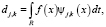
где R – интервал определения функции f(x). Переменная j характеризует уровень разложения, и ее часто называют коэффициентом масштаба, величина J определяет «глубину» разложения, а переменная k – временной сдвиг той или иной базисной функции. Заметим, что а) системы функций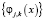 
, 
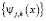составляют ортогональный базис пространств вейвлет-функций (подробнее см. [1, 4]); б) чем меньше номер j у базисных функций, тем более «мелкие» структуры исходной функции f(x) могут быть представлены в базисах 
, 
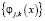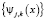и тем ближе реконструированный сигнал 
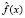к исходному. Обозначим коэффициенты разложения зашумленного сигнала 
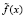как 
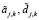. Заметим, что относительные погрешности аппроксимирующих коэффициентов на порядок и более меньше погрешностей коэффициентов 
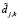(см. [4]). Поэтому на практике обработке подвергаются только детализирующие коэффициенты 
.
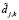Пороговая обработка коэффициентов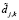 
на втором этапе вейвлет-фильтрации определяется используемой пороговой функцией. Широко используются «жесткая»
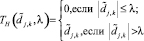(1)
и «мягкая»
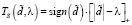(2)
пороговые функции [1, 4, 6], где λ – величина порога, а обозначение [z]+ определяется как
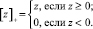
Пороговая величина λ существенно влияет на ошибку фильтрации и является «управляющим» параметром алгоритмов вейвлет-фильтрации. Сравнение различных алгоритмов выбора порога λ выполнено в [4]. Оценивание оптимального значения λopt, минимизирующего среднеквадратическую ошибку фильтрации рассмотрено в работах [4, 7]. Далее будем полагать, что величина λ задана равной λopt.
Пороговый характер обработки коэффициентов разложения приводит к тому, что часть «информативных» коэффициентов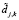 
(которые соответствуют ненулевым коэффициентам разложения dj,k незашумленного сигнала) зануляется и соответствующие базисные функции не участвуют в формировании отфильтрованного сигнала. Это обуславливает появление в окрестностях «скачков» амплитуд фильтруемого сигнала новых составляющих – артефактов, отсутствующих в обрабатываемом сигнале – некоторый аналог эффекту Гиббса, который проявляется при Фурье-фильтрации.
В качестве иллюстрации этого факта рассмотрим результаты вычислительного эксперимента по фильтрации одномерного дискретного «ступенчатого» сигнала (число отсчетов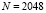 
), представляющего набор прямоугольных импульсов, зашумленные значения которого показаны на рис. 1. Относительный уровень шума
,
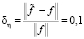где f – вектор, составленный из значений «точного» сигнала,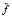 
– вектор «зашумленных» значений, 
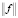– евклидова норма вектора. На рис. 2 показан результат вейвлет-фильтрации такого сигнала (использовалась пороговая функция (1)). Можно отметить достаточно хорошую фильтрацию шума на плоских участках сигнала, но появились артефакты – осцилляции в «особых» точках, где происходит резкое (скачкообразное) изменение амплитуды обрабатываемого сигнала. При этом значение относительной ошибки фильтрации
,
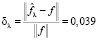где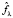 
– вектор, проекции которого определяются отфильтрованным сигналом. Вариация пороговой величины λ в приемлемом (с точки зрения общей ошибки фильтрации) интервале и использование пороговой функции (2) слабо повлияло на амплитуду и характер артефактов. Поэтому возникает задача об устранении (или существенном уменьшении) артефактов вейвлет-фильтрации. Для решения этой задачи добавим этап постобработки отфильтрованного сигнала локально-пространственными алгоритмами фильтрации.
Локально-пространственные алгоритмы фильтрации
Характерной чертой этих алгоритмов является то, что отфильтрованное значение определяется преобразованием значений исходного фильтруемого сигнала, попавших в апертуру (окно) фильтра. Такими преобразованиями может быть вычисление среднего значения, медианы или других числовых характеристик. Для обработки всего сигнала апертуру фильтра «перемещают» по обрабатываемому сигналу. Изменение размеров апертуры фильтра позволяет «управлять» точностными характеристиками алгоритма сглаживания в соответствии со следующим «правилом»: при увеличении размера апертуры увеличивается степень сглаживания случайного шума, но возрастает сглаживание контрастных деталей «точного» сигнала, которые желательно сохранить в отфильтрованном сигнале. При уменьшении апертуры наблюдается обратная картина.
Работу фильтров поясним на примере фильтрации зашумленного дискретного сигнала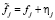 
, 
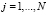, где ηj – случайный шум (погрешность) измерения с числовыми характеристиками: математическим ожиданием равным нулю и дисперсией σ2 (однородный шум измерений).
Фильтр скользящего среднего. Результат работы фильтра (обозначим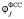 
) можно представить выражением
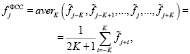(3)
где averK() – функция, которая вычисляет среднее значение из 2•L + 1 значений, указанных в скобках. Этот фильтр хорошо удаляет погрешности равноточных измерений. Очевидно, что, меняя размер апертуры K, можно варьировать степень сглаживания зашумленного сигнала, при этом дисперсия значения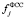 
равна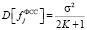 
. Следовательно, чем больше размер апертуры, тем сильнее сглаживание погрешностей измерения. Однако при этом в большей степени будут сглаживаться контрастные детали «точного» сигнала fj, которые необходимо сохранить в отфильтрованном сигнале. Заметим, что это противоречие характерно для всех линейных алгоритмов фильтрации.
Медианный фильтр. Результат работы фильтра (обозначим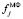 
) определим соотношением
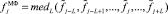, (4)
где medL() – функция, вычисляющая медиану из 2•L + 1 значений зашумленного сигнала, записанных в скобках. Медианный фильтр является уже нелинейным фильтром и имеет следующие особенности: сохранение в отфильтрованном сигнале контрастных деталей сигнала fj (при подходящем выборе размера апертуры); хорошая фильтрация импульсных шумов; значение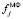 
медианного фильтра равно одному из значений 
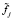, попавших в апертуру фильтра. Таким образом, сигнал 
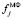содержит «остаточный» шум, который определяется погрешностями ηj, что обуславливает его низкую эффективность при фильтрации однородного шума измерений по сравнению с фильтром скользящего среднего.
Комбинированный фильтр [8]. Этот нелинейный фильтр можно трактовать как комбинацию «медианный фильтр + интервальный фильтр скользящего среднего», и для каждого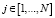 
выполняются следующие шаги:
Шаг 1. Вычисляется значение:
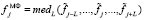. (5)
Шаг 2. Вычисляется результат работы комбинированного фильтра:
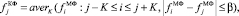(6)
где L, K – размер апертур фильтров, причем K ≥ L. Видно, что на втором шаге усредняются только те значения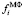 
, которые попали и в апертуру усредняющего фильтра, и в интервал 
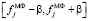, что сохраняет (при соответствующем выборе величины β) контрастные детали «точного» сигнала fj. Для выбора величины β можно воспользоваться правилом «двух сигм» [4]: 
.
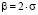Устранение артефактов алгоритмами локально-пространственной фильтрации
Свойство фильтров (4)–(6) хорошо фильтровать импульсные шумы позволяет надеяться, что, используя эти фильтры удастся удалить артефакты вейвлет-фильтрации. Проверим это предположение. Применим к вектору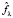 
(результат вейвлет-фильтрации – см. рис. 2) описанные выше алгоритмы (3)–(6) локально-пространственной фильтрации. На рис. 3 показаны проекции вектора 
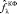– результат работы комбинированного фильтра (5), (6).
Параметры фильтров: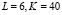 
. Видно, что комбинированный фильтр (5), (6) эффективно удалил как артефакты, так и «остаточный» шум (в отличие от медианного фильтра (4)), но сохранил при этом прямые углы вершин сигнала. Эти выводы подтверждают и вычисленные относительные ошибки фильтрации: 
, 
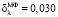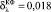(напомним, что относительная ошибка вейвлет-фильтрации δλ = 0,039).
На рис. 4 приведен результат вейвлет-фильтрации дискретного комбинированного сигнала – присутствуют «гладкая» и «ступенчатая» составляющие (относительный уровень шума 10 %, число отсчетов 2048 и относительная ошибка вейвлет-фильтрации δλ = 0,030). Снова видны артефакты в окрестностях ступенчатого изменения амплитуды сигнала и их отсутствие на «гладких» участках сигнала. На рис. 5 – результат работы комбинированного фильтра (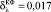
). Здесь наблюдается не только полное удаление артефактов, но и хорошая фильтрация остаточного шума вейвлет-фильтрации.
В таблице приведены средние значения относительных ошибок фильтрации прямоугольного сигнала для разных уровней шума с использованием жесткой пороговой функции (1) (обозначение TH) и предложенного метода (КФН). Видно существенное уменьшение ошибки фильтрации предложенным методом.
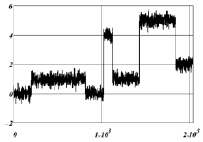
Рис. 1. Зашумленные значения ступенчатого сигнала
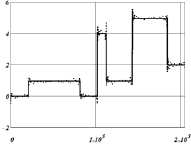
Рис. 2. Артефакты вейвлет-фильтрации
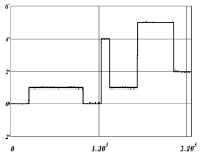
Рис. 3. Результат локально-пространственной фильтрации ступенчатого сигнала
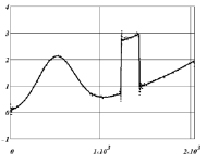
Рис. 4. Результат вейвлет-фильтрации комбинированного сигнала
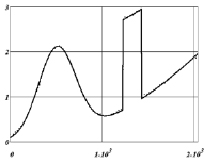
Рис. 5. Результаты локально-пространственной фильтрации комбинированного сигнала
Средние значения относительных ошибок фильтрации, в отн. ед.
|
Алгоритм фильтрации |
Уровни шума измерения |
||
|
0,02 |
0,05 |
0,10 |
|
|
TH |
8,48•10–3 |
0,020 |
0,039 |
|
КФН |
2,40•10–3 |
7,12•10–3 |
0,019 |
Заключение
Анализ рисунков и значений относительных ошибок фильтрации, приведенных в таблице, позволяет сделать вывод о целесообразности использования предложенного метода устранения артефактов вейвлет-фильтрации, который заключается в добавлении к алгоритмам вейвлет-фильтрации этапа постобработки с использованием нелинейных алгоритмов локально-пространственной фильтрации. К такому же выводу можно прийти, анализируя результаты вычислительного эксперимента с другими формами сигналов. Заметим, что этот метод легко обобщается на фильтрацию изображений (двумерных дискретных сигналов). В случаях, когда конечным результатом обработки являются коэффициенты вейвлет-разложения (например, в задаче сжатия информации), то требуемое вейвлет-разложение можно применить уже к результату локально-пространственной фильтрации, тем самым существенно увеличить точность вычисления коэффициентов разложения.