Изменения в технологиях телекоммуникаций и интенсивное развитие компьютерной техники привели к развитию телекоммуникационных систем (ТКС). Стремительное развитие возможностей вычислительной техники, необходимость обеспечения мобильной связи, электронного бизнеса и торговли, мультимедийных технологий и т.д. привело к появлению территориально рассредоточенных и сложных по структуре инфокоммуникационных сетей. Принятие эффективных управленческих решений в таких условиях становится крайне важным. Существенную помощь в принятии таких решений могут оказать такие разделы современной науки, как теория сложных систем, имитационное моделирование (ИМ) и экспертные системы.
Метод ИМ позволяет воссоздавать с определенной точностью процесс развития сложной системы, сохраняя законы ее функционирования и принимая во внимание стохастичность этого процесса. Имитационное моделирование позволяет воспроизвести состояние системы в любой требуемый момент времени, в том числе и при ограниченности исходной информации, недостаточно конкретизированных условиях и сложности формализации полученных данных.
При использовании имитационного моделирования в процессах управления изменение входных данных и параметров внешней среды позволяет получить различные реализации моделей; путем обработки этого множества решается проблема постановки задачи оптимизации, упрощается выбор параметров оптимизации [1].
Телекоммуникационные системы являются сложными системами. К таким системам относят системы автоматизированного управления, крупные производственно-технологические, телекоммуникационные комплексы, многопроцессорные вычислительные системы и другие объекты [2; 3].
Сложная система представляет собой совокупность отдельных частей со своими свойствами и закономерностями функционирования. Исследование подобной системы предполагает решение задач, связанных как со свойствами отдельных элементов, так и с функционированием этих элементов в рамках единой системы. Наиболее важную роль для исследования играют свойства элементов системы, определяющих отношение к другим элементам или всей системе в целом.
В качестве примера сложной телекоммуникационной системы можно рассматривать городские телефонные сети [4]. Сети такого рода включают инфосетевые технологии (коммутационные блоки телефонных станций, системы централизованного автоматического обслуживания, биллинговые системы и т.п.), телекоммуникационное аппаратное обеспечение (пользовательское оконечное оборудование, аппаратура автоматических телефонных станций, модемы, маршрутизаторы, кабельные системы) и соответствующие услуги (обеспечение доступа к телефонным сетям и к сети Интернет, предоставление услуг мобильной телефонии). Таким образом, процесс работы телефонной сети – наглядный пример функционирования современной сложной системы.
В вопросах функционирования сложных систем немаловажное значение имеет управление. Управление представляет собой выработку целенаправленного функционирования сложной системы путем определенных воздействий, формируемых различными средствами. Замкнутость контуров управления предполагает наличие обратной связи, то есть при отклонении реального значения какого-либо параметра от заданного формируется соответствующий управляющий сигнал.
Средствами формирования таких управляющих воздействий для реальных ТКС выступают различные устройства вычислительной техники, обеспечивающие обработку фактических значений контролируемых параметров и планирование соответствующих корректирующих воздействий. Долгосрочное планирование и оперативное управление процессами функционирования сложных систем должно выполняться в рамках управляющего алгоритма. Управляющий алгоритм может быть как централизованным, так и распределенным или децентрализованным. Качественно выполненная децентрализация управляющего алгоритма позволяет сократить объемы обрабатываемой информации и время отклика на корректирующие воздействия. В обратном случает качество управления может значительно снизиться.
На процессы функционирования всех сложных систем в реальных условиях влияют многочисленные случайные факторы. К подобным факторам относят влияние внешней среды и внутрисистемные искажения, связанные с физическими законами передачи информации. Внешние и внутренние факторы приводят к различным отклонениям от заданных величин. В ТКС такими факторами могут быть непредвиденные пиковые нагрузки, к которым приводят одновременные требования абонентов на телефонные переговоры, внезапные сложно прогнозируемые перераспределения трафика, неожиданные включения или отключения потребителей электроэнергии и т.п. [1].
Режим работы компонентов системы существенно зависит от различных случайных воздействий, как внешних, так и внутренних, оказывая значительное влияние на функционирование системы. Математическое описание этого процесса хорошо изучено [5].
Всякая сложная система создается как целевая совокупность объектов для выполнения определенного типа работ и/или решения некоторого класса задач. Корректный и исчерпывающий анализ требований к функционированию сложной системы имеет определяющее значение. Оценка качества функционирования системы, как самостоятельная задача, возникает при условии определенности функциональных требований к системе. Показатели эффективности являются критериями оценивания качества функционирования сложных систем. Показатель эффективности при этом представляют как некоторую численную характеристику, определяющую соответствие системы для решения возникающих задач [2, 5].
Показателями эффективности могут служить: производительность, измеряемая объемом трафика, пропускаемого каналом в течение фиксированного интервала; пропускная способность канала, достоверность передачи данных, а также другие аналогичные характеристики работы ТКС. Описание целей и задач системы невозможно без выбора показателя эффективности. Этот выбор зависит от структуры и параметров системы, влияния внешней среды, воздействия внешних и внутренних случайных факторов.
Очевидно, что может существовать множество возможных вариантов функционирования компонентов системы, с разнообразными условиями и режимами работы. Каждому такому варианту соответствуют определенные показатели эффективности функционирования системы. Множество процессов функционирования системы отображается в множество действительных чисел в интервале изменения численных значений показателя эффективности. Таким образом, показатель эффективности является функционалом [1].
Известно, что сложные системы функционируют в условиях случайных воздействий, и, следовательно, значения функционалов являются случайными. Поэтому при оценке показателей эффективности используют усредненные значения данных функционалов [5].
Функционалы в качестве показателей эффективности могут быть применены для характеристики различных свойств сложных систем, таких как их помехозащищенность, надежность, реакция обратной связи и др. Группы функционалов, которые напрямую зависят от показателей эффективности, отличаются наибольшей наглядностью с точки зрения представления результатов исследования, т.к. значение имеют те свойства системы, которые влияют на ее эффективность.
Каждая сложная система образует совокупность большого количества элементов, которые в процессе эксплуатации могут приходить в негодность, что влечет за собой замену либо ремонт. Оценка отказоустойчивости элементов определяет параметры надежности работы системы, – показатели надежности системы.
В реальных системах возможность выхода из строя критически важных элементов является заранее прогнозируемым с некоторой вероятностью событием, и в результате применения механизмов резервирования не приводит к потере работоспособности всей системы в целом. Такими событиями могут быть, например, выход из строя линий связи в абонентской сети, отказы одного или нескольких каналов в многоканальных системах массового обслуживания (СМО) [1].
Качественное и количественное развитие компьютерной техники и цифрового оборудования, а также использование новых информационных технологий создали возможные и необходимые условия для использования в задачах управления ТКС многих ресурсоемких методик исследования, а именно имитационного моделирования.
Возможности современных электронно-вычислительных машин и комплексов на их основе позволяют реализовать эффективный человеко-машинный диалог, что является необходимым условием успешного применения методов ИМ. Методы ИМ позволяют воспроизводить и анализировать различные процессы без существенного снижения их сложности.
Имитационная модель является аналогом реально происходящего сложного процесса. Она дает возможность проводить эксперимент с реализацией математической модели этого процесса на ЭВМ, исключая эксперимент с реальным процессом.
Многие системы, моделируемые с помощью имитационных методов, предполагают использование в своей основе метода Монте-Карло. Данный метод позволяет рассматривать большое количество возможных реакций системы на внешние воздействия и прогнозировать вероятность их возникновения [6].
Моделируемые сложные ТКС относятся к системам массового обслуживания, для которых разработаны многочисленные алгоритмы [7].
Моделирующий алгоритм должен не только адекватно и полно отображать процесс функционирования СМО, но и в то же время обладать приемлемой вычислительной сложностью для его реализации на ЭВМ и использования. Таким образом к моделирующему алгоритму выдвигаются следующие требования:
- моделируется одновременная и независимая работа любого количества элементов;
- малые затраты ресурсов ЭВМ на реализацию;
- простота реализации алгоритма, возможность декомпозиции на независимые модули, максимальная стандартизация.
Большое количество СМО требует создания различных моделирующих алгоритмов. Классифицировать эти алгоритмы [5; 7] возможно лишь условно, так как при моделировании крупной системы возможно применение частей различных алгоритмов (рисунок). Все применяемые в настоящее время моделирующие алгоритмы могут использоваться для СМО. Следовательно, модель сложной телекоммуникационной системы, рассматриваемой как система массового обслуживания, также может быть описана каким-либо моделирующим алгоритмом. Выбор алгоритма варьируется в зависимости от сложности реализации, затрат машинных ресурсов и других параметров.
Представляя ТКС как сложную производственную систему, можно сделать вывод о функционировании в ней следующих агрегированных групп оборудования: непрерывный агрегат, дискретный агрегат, дискретно-непрерывный агрегат [7; 8].
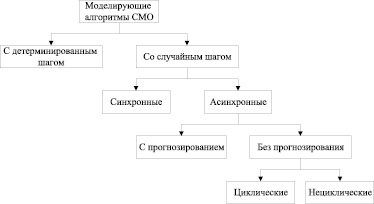
Классификация моделирующих алгоритмов СМО
Входным управляющим сигналом и выходным сигналом для ТКС, как сложной производственной системы, является информация.
Анализ функционирования показывает, что ТКС является дискретно-непрерывным агрегатом, так как множество случайных событий приводит к смене ее поведения [8].
Среди дискретно-непрерывных агрегатов можно выделить подклассы, для которых возможно получение простого решения. К типичным примерам дискретно-непрерывных агрегатов можно отнести математическую модель системы массового обслуживания. Следовательно, имитационное моделирование процессов ТКС может основываться на соответствующих моделях и алгоритмах СМО.
Однако исследование зависимости условий работы ТКС от времени усложняется настолько, что без применения компьютера его провести невозможно. Необходима модель, которая учитывает случайные обстоятельства функционирования СМО.
Практическую ценность имеет только анализ работы СМО в зависимости от времени. Решение данной задачи возможно только с применением современных электронно-вычислительных машин. При работе СМО возникают различные случайные события, которые имеют статистический характер. Таким образом, для моделирования ТКС необходимо использовать методы имитационного и статистического моделирования, в частности метод Монте-Карло.
Имитационное моделирование сложной телекоммуникационной системы с использованием ЭВМ можно представить следующими этапами [5; 7]:
1. Определение перечня исходных данных, оказывающих существенное влияние на функционирование исследуемой системы.
2. Анализ входных данных с целью выявления законов распределения. По результатам анализа могут быть получены как теоретическое распределение, так и эмпирическое, из которого в последующем можно генерировать выборки входных данных, необходимые для моделирования работы системы [5; 6; 7].
3. Определение законов распределения входной информации и вычисляются статистические оценки параметров этих законов.
4. Создание математических моделей модулей сложной системы и всего исследуемого процесса в целом; модели реализуются на ЭВМ.
5. Формирование плана эксперимента для имитации исследуемого процесса на ЭВМ.
6. Имитация процесса.
7. Формирование на каждой итерации моделирования предварительных результатов, которые используются для получения окончательных результатов.
8. Достижение либо требуемой доверительной вероятности, либо указанного количества реализаций в качестве критерия завершения эксперимента. По результатам эксперимента делаются выводы и принимается управленческое решение.
Таким образом, рассматривая проблему управления сложными системами, можно сделать вывод, что иерархичность структуры и самоорганизация являются основополагающими признаками для создания моделей ТКС. Моделируя ТКС, следует принимать во внимание большое количество случайных факторов, от которых зависит эффективность ее работы. Критериями оценки эффективности работы ТКС могут быть такие интегральные показатели, как устойчивость, надежность, производительность, помехозащищенность. С математической точки зрения на множестве процессов функционирования ТКС показатель эффективности задается функционалом.
Увеличение доли применения математических методов в практике моделирования и значительный рост производительности современных ЭВМ привели к тому, что формализация и исследование сложных процессов (технических, производственных, экономических), происходящих в ТКС, стали реальной задачей. Имитационное моделирование с применением ЭВМ стало наиболее подходящим методом для анализа функционирования и управления подобными системами. Таким образом, разрабатываемая система моделирования представляет собой комплекс из модели, имитирующей исследуемый процесс на ЭВМ, и соответствующего программного обеспечения. Таким образом эксперимент с реальным процессом заменяется реализацией математической модели этого процесса на ЭВМ.
Подводя итог, можно сделать вывод о применимости ИМ для решения задач управления сложными ТКС. Вычислительные мощности современных ЭВМ позволяют эффективно использовать методы и средства теории сложных систем для ИМ ТКС. В частности, для моделирования условий работы ТКС при воздействии случайных факторов целесообразно применять метод Монте-Карло, который лежит в основе группы эффективных методов исследования сложных процессов и систем. При реализации на ЭВМ метода Монте-Карло результаты ИМ представляют собой числовые последовательности выходных данных, которые необходимо статистически обработать и в последующем интерпретировать.
Кроме того, для имитационного моделирования современных ТКС может быть применен математический аппарат СМО. Известные алгоритмы, моделирующие работу СМО, отличаются сложностью реализации, затратами машинных ресурсов и другими параметрами. Следовательно, в рамках выбранной методики ИМ, необходимо в каждом случае делать аргументированный выбор моделирующего алгоритма, от которого зависит достоверность результатов имитационного моделирования сложной ТКС и, соответственно, стратегия управления.



