Необходимость повышения точности расчета коэффициентов гидравлического сопротивления при течении жидкостей в трубах с различной степенью песочной шероховатости внутренней поверхности стенки трубы требует дальнейшего обобщения опытных данных и, на их основе, совершенствования инженерных методов расчета. Основой для анализа являются опытные данные Никурадзе по движению ньютоновской жидкости в гладких и шероховатых трубах, приведенные, например, в работе [9]. На основании анализа этих опытных данных, с привлечением гипотез Прандтля, Кармана и других исследователей о физической природе турбулентного движения жидкости, получены достаточно простые аналитические выражения, позволяющие определить коэффициенты гидравлического сопротивления и профиля скорости в двух предельных случаях: гидравлически гладкой стенки (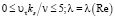
) и режима течения с полным проявлением шероховатости 
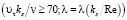. Здесь λ – коэффициент гидравлического сопротивления; υτ – динамическая скорость; ν – кинематическая вязкость жидкости; ks – величина песочной (эквивалентной) шероховатости стенки; R – радиус трубы; 
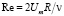– число Рейнольдса, определенное по средней скорости Um и диаметру (2R).
В значительно меньшей степени исследованы режимы течения жидкости при переходном режиме
.
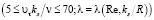Проанализируем работы, выполненные в последние годы. В работах [2, 3], используя, формулы Прандтля и Кармана для коэффициентов гидравлического сопротивления гидравлически гладкой и предельно шероховатой поверхности
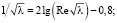(1)
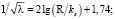(2)
и известные логарифмические зависимости распределения скоростей для гидравлически гладких и предельно шероховатых труб, с использованием выражений (1) и (2) приведены к близким зависимостям
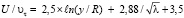, (3)
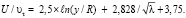(31)
Обе зависимости практически идентичны и получены без приведения, каких-либо выражений для расчета λ при переходном режиме течения и даже обсуждения этого вопроса.
Автор не приводит выражения для расчета коэффициента гидравлического сопротивления, а, видимо, использует их опытные значения, получает удовлетворительное соответствие для ограниченного числа опытных данных по профилю скорости.
В работе [7] расчетная схема включает прилегающий к стенке вязкий подслой, переходящий в турбулентную зону смешения с постоянной длиной смешения. В области выше элементов шероховатости реализуется турбулентный режим течения с длиной пути смешения, зависящий от расстояния от поверхности. Заметим, что такая схематизация течения жидкости вдоль шероховатой поверхности ранее использовалась в работе [6] для расчета течения не только в ньютоновской жидкости, но и для неньютоновских жидкостей. Автор сравнивал результаты расчетов не с опытными данными Никурадзе, а с расчетом по формуле Колбрука – Уайта, которая, как известно [10], применима не к песочной, а к технической шероховатости. Кроме того, сравнение расчетных данных проводилось при больших числах Рейнольдса от области минимального значения коэффициента гидравлического сопротивления до максимального, соответствующего режиму с предельным проявлением шероховатости. Например, выпал из рассмотрения диапазон чисел Рейнольдса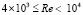 
для частиц с максимальной песочной шероховатостью R/ks = 15, а для частиц с минимальной шероховатостью R/ks = 507 не рассмотрен диапазон чисел Рейнольдса 
.
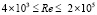В работе [4] автор предлагает рассчитывать коэффициент гидравлического сопротивления при переходном λt, гладком λ и квадратичном λs режимах сопротивления по формуле, выражающей принцип суперпозиции:
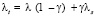, (4)
где γ – коэффициент перемежаемости, равный отношению времени существования турбулентного течения у стенки к общему времени наблюдения. Именно такая зависимость ранее использовалась в [6], где величина γ физически толковалась как доля поверхности, течение над которой соответствует режиму течения над гидравлически гладкой поверхностью, а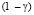 
течению над поверхностью с предельным проявлением шероховатости. Затем, не имея достаточных оснований, выражение (2) записывается в виде [4]
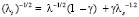. (41)
Полученные результаты вызывают сомнение, поскольку с равным успехом можно было подобрать эмпирическую зависимость, соответствующую выражению (4).
В большинстве из рассмотренных работ [2–4, 7] использовались логарифмические профили скорости для гидравлически гладкой и предельно шероховатой стенки трубы и соответствующие им зависимости коэффициентов гидравлических сопротивлений, а затем они обобщались на случай переходной режим. В работе [8], в рамках традиционной схемы течения над шероховатой поверхностью [9], выражение для скорости с произвольной степенью песочной шероховатости поверхности записывается в виде
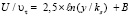, (5)
где величина B зависит от режима обтекания поверхности.
При переходном режиме используется известная зависимость
;
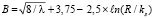при 0,025 < ks/ δ< 5 и 3 < υτks/ν < 70. (6)
Также как в работе [7] закон сопротивления при переходном режиме задается формулой Колбрука – Уайта
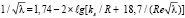, (7)
что, как отмечалось выше, физически некорректно [9]. Поэтому расчеты течения в круглой трубе приведут к тем же ограниченным результатам, которые были получены в работе [7].
Следует отметить, что при использовании выражения (7) и подобной, наиболее простой в части процедуры вычислений, формуле Альтшуля [1]
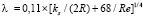(8)
величина λ плавно уменьшается с ростом числа Рейнольдса, то есть полностью игнорируется наличие минимума величины λ, зависящее от обеих величин ks/(2R) и Re. Игнорирование этого опытного факта представляется весьма существенным, в связи с чем все конкретные рекомендации по расчету профиля скорости в этой зоне представляются недостаточно обоснованными.
В работе [10] автор показывает, что формулы Прандтля и Колбрука – Уайта, соответственно, могут быть выражены в виде функции Ламберта, зависящей только от величин ks/(2R) и Re. Использование функции Ламберта в чисто вычислительном аспекте не имеет никакого преимущества перед использованием классических выражений в области их применимости.
Покажем, что имеющихся опытных данных вполне достаточно для определения профилей скорости и коэффициентов гидравлического сопротивления при течении жидкости в круглых трубах. Основываясь на предварительном анализе, обобщим выражение для коэффициента гидравлического сопротивления (7), записывая его в виде
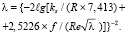(9)
где f – поправочная функция, зависящая от безразмерного комплекса (ksυτ/ν). Основанием для такого предположения является то, что, согласно опытным данным [9], величина B зависит от безразмерной переменной величины lg(ksυτ/ν).
Проведенные расчеты показали, что удовлетворительное соответствие с опытными данными по коэффициенту гидравлического сопротивления имеет место при следующем виде поправочной функции
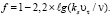(10)
На рис. 1 показано сравнение опытных и расчетных величин λ по формулам (9), (10). В диапазоне чисел Рейнольдса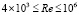 
, расчетные значения λ хорошо согласуются с опытными данными в трубах с песочной шероховатостью стенки трубы, причем это относится и к положению минимального значения величины λ при величине относительной шероховатости в пределах 
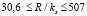. Расчетные значения величины λ для технической шероховатости R/ks = 1300 также удовлетворительно согласуются с опытными данными.
Число Рейнольдса, при котором шероховатую поверхность надо считать гидравлически гладкой, определим из условия равенства величин λ, рассчитываемых по формулам (1) и (9) [5]. В таблице приведены значения чисел Рейнольдса при различной степени песочной шероховатости стенки трубы.
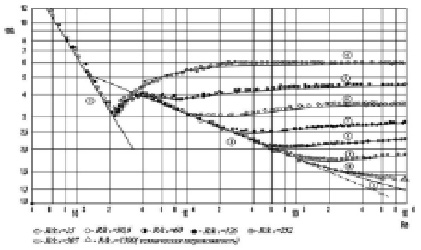
Рис. 1. Закон сопротивления для гладких и шероховатых труб. Кривая 1 соответствует ламинарному режиму течения. Кривая 2 соответствует формуле Блазиуса. Кривая 3 соответствует формуле Прандтля. Кривые 4–10 расчет по формуле (9)
Граница перехода течения с гидравлически гладкого на переходной режим
|
R/ks |
15 |
30,6 |
60 |
126 |
252 |
507 |
1300 |
|
Re |
– |
4, 58×103 |
104 |
2,32×104 |
5,15×104 |
1,12×105 |
9,5×104 |
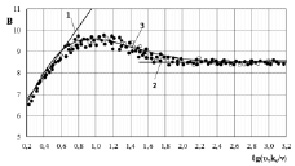
Рис. 2. Зависимость величины В от lg(υτks/ν).. Кривая 1 соответствует режиму без проявления шероховатости. Кривая 2 соответствует режиму с полным проявлением шероховатости. Кривая 3 – расчет по формуле (6)
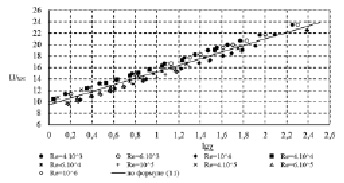
Рис. 3. Расчетные значения относительной скорости U/υτ, определенные по формуле (5), и их аппроксимация по формуле (11)
Используя расчетные значения λ можно рассчитать величину В по формуле (6). На рис. 2 представлены результаты расчетов величины B по (8) при различной степени песочной шероховатости.
Профиль относительной расчетной скорости U/υτ в трубе с произвольной песочной шероховатостью стенки трубы определяется по формуле (5), в которой величина B рассчитывалась по (6), а величина λ по (9), (10). В качестве абсциссы использовался предложенный в [1] безразмерный параметр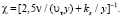 
Расчет профиля скорости является важной задачей, но конечной практической целью расчетных исследований, как правило, является определение коэффициентов гидравлического сопротивления, при которых использование инженерных аналитических зависимостей представляется предпочтительным.
Результаты численных расчетов с погрешностью 10 % аппроксимируются зависимостью
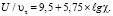(11)
Отметим, что ранее нами была рассмотрена эта же задача [5], при решении которой вначале была предложена эмпирическая зависимость для расчета величины В, а затем рассчитывался коэффициент гидравлического сопротивления и профиль относительной скорости. В вычислительном плане предложенная аппроксимация (10) значительно упрощает процедуру расчета.