В результате сложного взаимодействия волн с рельефом дна, береговой линией и различными объектами наблюдается их рефракция, дифракция и изменения структуры береговой зоны. Возникает необходимость в построении математических моделей, учитывающих особенности рельефа дна прибрежной акватории и наличие надводных сооружений. Не приуменьшая целесообразности использования трехмерных моделей волновых гидродинамических процессов [8–11], следует подчеркнуть важность разработки двумерных моделей гидродинамики при исследовании воздействия волн на надводные объекты, на основе данных моделей при приемлемой точности можно производить оперативные численные расчеты, при условии ограниченности вычислительных ресурсов. Полученные численные результаты распространения гидродинамических колебаний позволят провести оценку воздействия волн на объекты, находящиеся в прибрежной зоне мелководных водоемов.
Постановка задачи волновой гидродинамики
Для построения двумерной математической модели движения водной среды использовалась трехмерная гидростатическая модель. Исходными уравнениями гидродинамики являются:
– система уравнений Навье – Стокса
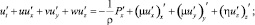
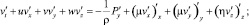(1)
– уравнение неразрывности для несжимаемой жидкости
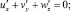(2)
– уравнение гидростатики
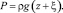(3)
Система уравнений (1)–(3) рассматривается при следующих граничных условиях: на дне условие непроницаемости и трения [2–5]
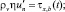
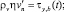Vn = 0,
на поверхности задается подъем уровня и ветровые напряжения
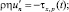
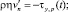
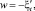
на боковых границах условие скольжения без трения
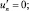
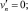
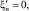
где ξ – функция подъема уровня (функция возвышения); V = {u, v, w} – вектор скорости движения водной среды; P – давление; μ, η – коэффициенты турбулентного обмена по горизонтальному и вертикальному направлениям соответственно; g – ускорение свободного падения; ρ – плотность жидкости; τx, τy – тангенциальное напряжение на дне жидкости.
Уравнение расчета давления в гидростатическом приближении при наличии надводной конструкции, установленной на дне водоема:
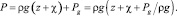
Доопределим функцию возвышения в случае наличия на поверхности надводного тела:
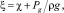
где χ – функция, описывающая геометрию дна надводного тела.
В уравнение неразрывности (2) в гидростатическом случае запишем в виде
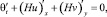(4)
где θ = min(χ, ξ); H = h + θ; h – глубина водоема.
Система уравнений (1) с учетом гидростатического приближения в двумерном случае имеет вид
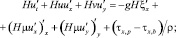
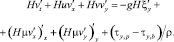(5)
Предложенная двумерная модель волновых гидродинамических процессов описывает поведение водной среды как в случае наличия надводной конструкции, установленной на дне водоема, так и в случае ее отсутствия.
Дискретная модель гидродинамики
Область моделирования вписана в прямоугольник и покрыта равномерной прямоугольной расчетной сеткой ω = ωt×ωx×ωy:
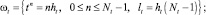
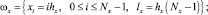
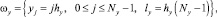
где n, i, j – индексы по временной координате и пространственным координатным направлениям Ox, Oy соответственно; ht, hx, hy – шаги по временной координате и пространственным координатным направлениям Ox, Oy соответственно; Nt, Nx, Ny – количество узлов по временной координате и пространственным координатным направлениям Ox, Oy соответственно; lt, lx, ly – длина расчетной области по временной координате и пространственным координатным направлениям Ox, Oy соответственно.
Расчетные ячейки представляют собой прямоугольники, они могут быть заполненными, частично заполненными или пустыми [11]. Поле скоростей и давление рассчитываются в вершинах ячейки. Центры ячеек и узлы разнесены на hx/2 и hy/2 по координатам x и y соответственно. Обозначим через oi,j «заполненность» ячейки (i, j). Вершинами ячейки (i, j) являются узлы (i, j), (i – 1, j), (i, j – 1), (i – 1, j – 1). Вводятся коэффициенты q0, q1, q2, q3, q4, описывающие «заполненность» областей, находящихся в окрестности ячейки. Коэффициенты qm можно вычислить по формулам
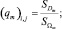
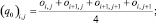
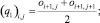
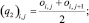
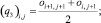
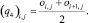(6)
Рассмотрим двумерную модель движения водной среды, представленную уравнениями (4), (5). Воспользуемся схемами расщепления по физическим процессам [1–4] для системы (5). При этом решения задачи находим вначале на некоем промежуточном временном слое:
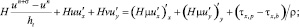
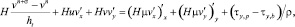(7)
затем на следующем временном слое
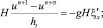
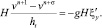(8)
Для решения задачи (8) вычислим функцию возвышения уровня, дифференцируя первое уравнение системы по переменной x, второе по переменной y, сложив их, имеем
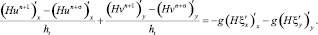
Полученное выражение с учетом уравнения неразрывности примет вид
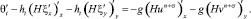(9)
Дискретные аналоги операторов конвективного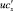 
и диффузионного 
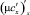переноса, учитывающие частичную заполненность ячеек, в случае граничных условий третьего рода 
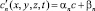запишем в следующем виде:
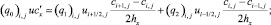
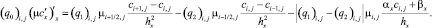
Полученные сеточные уравнения решены на основе адаптивного модифицированного попеременно-треугольного итерационного метода вариационного типа [4, 6, 7].
Измерение параметров волновых процессов на основе натурных наблюдений
Проведен натурный эксперимент по измерению различных параметров распространения волны на мелководье. На основе экспериментальных данных получены значения спектра функции возвышения уровня водной среды. Для обработки результатов натурных измерений использован тригонометрический интерполяционный полином. Расчет коэффициентов ряда Фурье выполнен согласно выражению
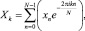
где [xn] – заданная последовательность чисел с постоянным шагом дискретизации размерности N.
С учетом обозначений: a = Rex, b = Imx, тригонометрическая функция, проходящая через точки {n, xn}, примет вид
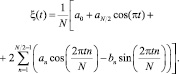
На рис. 1 точками отмечены значения спектра волны, линиями представлены функции, распределенные по нормальному и логнормальному законам и имеющие математические ожидания и дисперсии, соответствующие реальным натурным данным.
На рис. 2 красным представлена функция, распределенная по логнормальному закону, синим – функция, распределенная по нормальному закону, черным – реальные натурные значения функции возвышения уровня.
В таблице приведены значения глубин, на которых проводились измерения, а также значения периода волны, средняя и максимальная высота волны, дисперсии функции возвышения уровня, зависящей от глубины, а также значение коэффициентов корреляции с нормальным и логнормальным распределениями.
Волновые процессы по большей части можно описать тремя величинами: математическим ожиданием (период волны), дисперсией и амплитудой нормального или логнормального распределения компонент спектра. Эти величины получены при обработке данных натурного эксперимента и используются в качестве граничных условий для математических моделей волновых гидродинамических процессов.
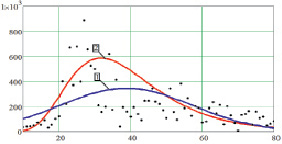
Рис. 1. Спектр функции возвышения уровня: 1 – нормальное распределение; 2 – логнормальное распределение
Рис. 2. Сопоставление результатов измерений с нормальным и логнормальным распределением
|
№ п/п |
Глубина, см |
Период волны, с |
Средняя высота волны, см |
Максимальное значение высоты волны, см |
Дисперсия функции возвышения уровня |
Корреляция с нормальным распределением |
Корреляция с логнормальным распределением |
|
1 |
12,734 |
3,181 |
1,434 |
3,266 |
3,384 |
0,67622403 |
0,72818161 |
|
2 |
21,657 |
3,187 |
2,216 |
5,127 |
2,875 |
0,71970734 |
0,75497854 |
|
3 |
34,296 |
3,257 |
2,673 |
6,673 |
2,587 |
0,76756352 |
0,80809736 |
|
4 |
47,696 |
3,208 |
2,903 |
7,278 |
2,373 |
0,80434285 |
0,81516631 |
|
5 |
50,221 |
3,238 |
3,408 |
8,779 |
2,465 |
0,80072646 |
0,82234947 |
|
6 |
56,95 |
3,323 |
3,423 |
10,05 |
2,539 |
0,82520735 |
0,83499856 |
|
7 |
58,256 |
3,094 |
3,538 |
13,742 |
2,468 |
0,70451786 |
0,75010325 |
|
8 |
75,284 |
3,482 |
3,595 |
12,716 |
2,317 |
0,80464887 |
0,82816629 |
|
9 |
83,353 |
3,056 |
4,472 |
14,647 |
2,498 |
0,7677805 |
0,80442466 |
|
10 |
123,251 |
3,23 |
4,671 |
15,749 |
2,327 |
0,78716382 |
0,82809779 |
Результаты численных экспериментов
Разработан комплекс программ, предназначенный для моделирования распространения волновых гидродинамических процессов, который позволяет задавать форму и интенсивность источника колебаний, а также геометрию надводного объекта. Результаты численных экспериментов по моделированию распространения волновых гидродинамических процессов при обтекании надводного тела водной средой с учетом геометрии дна объекта, находящегося в жидкости, и дна водоема приведены на рис. 3.
В качестве примера практического использования проблемно-ориентированного комплекса программ решается задача расчета гидродинамического воздействия волн опоры на сооружения. Размеры надводной конструкции: ширина 5 м, длина 10 м, глубина погружения 20 см. Конструкция установлена на дне водоема при помощи шести опор. Выделенный участок моделирования имеет размеры 50 на 50 м и глубину 1 м. Источник возмущений задается на некотором расстоянии от надводного объекта. В начальный момент времени жидкость находится в состоянии покоя. Требуется определить последующее движение водной среды при наличии на поверхности надводного объекта и силовые гидродинамические нагрузки на опоры сооружения. Для решения поставленной задачи использована сетка размерами 100×100, шаг по времени равен 0,01 с.
Рисунки иллюстрируют, что при распространении плоской волны, которая встречает препятствие в виде надводного тела, происходит отражение волновых колебаний от неподвижного объекта, что в свою очередь приводит к изменению профиля волны. Источник колебаний распределен по левой границе и имеет синусоидальную форму. Разработанный программный комплекс при моделировании распространения поверхностных колебаний учитывает выход волны на берег (рис. 5).
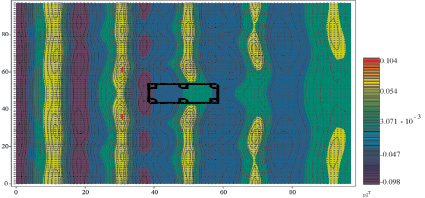
Рис. 3. Движение водной среды
Рис. 4. Функция возвышения уровня при обтекании водной средой надводного тела, имеющего опору
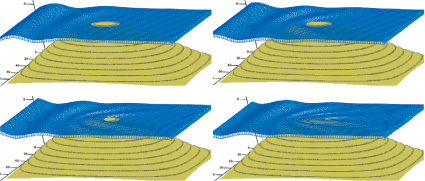
Рис. 5. Результаты расчета по распространению волновых колебаний
Заключение
Работа посвящена разработке двумерной модели, учитывающей гидродинамическое воздействие на различные надводные береговые сооружения при наличии поверхностных волн в мелководных водоемах. На основе экспериментальных данных получены значения спектра функции возвышения уровня водной среды. Из результатов экспериментальных наблюдений по изучению волновых процессов сделан вывод о том, что колебания поверхности водной среды могут быть описаны тремя величинами: математическим ожиданием, дисперсией и амплитудой нормального или логнормального распределения компонент спектра. Результаты численных экспериментов по моделированию распространения гидродинамических волновых процессов дают возможность провести оценку воздействия волн на сооружения, имеющие опору на дне водоема.
Работа выполнена при финансовой поддержке РФФИ по проектам № 16-37-00129, № 15-07-08626, № 15-01-08619.