Обеспечение отказоустойчивой работы авиационных газотурбинных двигателей (ГТД) – одна из основных задач адаптивных цифровых систем автоматического управления (САУ), эффективность решения которой во многом определяется выбранной методологией идентификации приближения к границе устойчивости [3]. Одним из признаков нарушения устойчивости газовых систем с компрессором, к которым относится ГТД, является наличие пульсаций потока во всасывающем или нагнетательном трубопроводе [2]. Причиной таких колебаний может быть приближение к помпажному режиму, характеризующемуся большими динамическими нагрузками, которые могут привести к разрушению компрессора. Таким образом, актуальной является задача алгоритмического управления предпомпажными режимами работы ГТД, адаптированного к границам его устойчивости. При этом верхняя граница устойчивой работы определяется срывом потока и автоколебаниями в компрессоре, а нижняя – срывом горения в малоэмиссионной камере сгорания. В настоящей работе рассматривается возможность идентификации предсрывных явлений в компрессоре на основе применения полосовых фильтров.
Целью исследования является разработка алгоритмов полосовой фильтрации, позволяющих наделить САУ ГТД функциями обнаружения предсрывных явлений в компрессоре, характеризующих приближение к границе помпажа.
В настоящее время наиболее характерным признаком предсрывных явлений принято считать [5] нарастание амплитуды пульсаций давления над рабочим колесом на частоте f = 0,6·n·z, где n – частота вращения ротора компрессора («роторная частота»), а z – число лопаток в рабочем колесе (очевидно, что f = n·z – «лопаточная частота») (рис. 1).
Таким образом, задача сводится к идентификации появления пиков пульсации давления на указанных частотах, характеризующих приближение к границе устойчивости, что требует расширения возможностей САУ ГТД.
Одним из путей решения задачи является применения алгоритмов полосовой фильтрации. Применяемый в данной работе метод полосовой фильтрации строится на объединении цифровых фильтров низких частот (ФНЧ) и фильтров высоких частот (ФВЧ).
Известно, что основной характеристикой фильтра является его импульсная характеристика (или ядро фильтра). При этом импульсная характеристика ФВЧ, равная k1(t), может быть определена через известную импульсную характеристику ФНЧ, равную k2(t), методом спектральной инверсии [1].
Полученный сигнал пульсаций давления ΔP(t) может быть интерпретирован как наложение высокочастотной ΔP1(t) и низкочастотной ΔP2(t) составляющих:
ΔP(t) = ΔP1(t) + ΔP2(t). (1)
Для выделения низкочастотной составляющей применяется операция свертки:
ΔP2(t) = ΔP(t)·k2(t). (2)
С учетом основного свойства свертки
x(t) = x(t)·δ(t),
где δ(t) – дельта-функция Дирака, получим из (1) и (2) для высокочастотной составляющей сигнала:
ΔP1(t) = ΔP(t) – ΔP2(t) = = ΔP(t)·δ(t) – ΔP(t)·k2(t) = = ΔP(t)·(δ(t) – k2(t)) = ΔP(t)·k1(t). (3)
Таким образом, из (3) следует, что импульсная характеристика ФВЧ равна
k1(t) = δ(t) – k2(t). (4)
Импульсная характеристика полосового фильтра k(t) определяется через свертку:
k(t) = k2(t)·k1(t). (5)
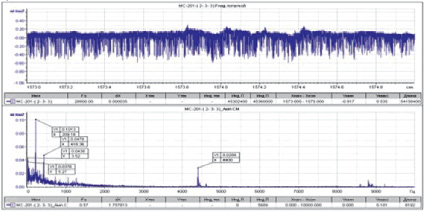
Рис. 1. Пульсации давления над рабочим колесом первой ступени при приближении к границе устойчивости во временной и частотной областях
По известной формуле связи между импульсной характеристикой и передаточной функцией полосового фильтра W(p) = L[k(t)] с помощью (4) и (6) определяется передаточная функция ФВЧ, имеющего ту же частоту среза, что и рассматриваемый ФНЧ:
W1(p) = L[k1(t)] = = L[δ(t) – k2(t)] = 1 – W2(p). (6)
В соответствии с (5), передаточная функция полосового фильтра может быть найдена по теореме о свертке:
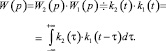(7)
При этом ФВЧ и ФНЧ имеют соответственно частоты среза f1 и f2.
Таким образом, по выбранной передаточной функции ФНЧ, для заданной полосы пропускания частот [f1; f2] по формулам (6) и (7) может быть построен полосовой фильтр (ПФ).
Известно, что простейший ФНЧ имеет переходную характеристику:
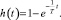(8)
По известной формуле связи между переходной и импульсной характеристикой k2(t) = h′(t) в соответствии с (8) может быть найдена импульсная характеристика проектируемого ФНЧ:
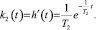(9)
где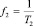 
(Гц) – частота среза ФНЧ и верхняя граница полосы пропускания ПФ.
Из (10) может быть определена передаточная функция проектируемого ФНЧ:
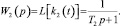(10)
Полученная W2(p) соответствует апериодическому звену первого порядка.
По формуле (6) определяется передаточная функция проектируемого ФВЧ с частотой среза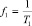 
(Гц), соответствующей нижней границе полосы пропускания ПФ:
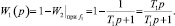(11)
Полученная передаточная функция W1(p) соответствует реальному дифференциальному звену первого порядка.
Согласно (7), (10) и (11) может быть получена результирующая передаточная функция ПФ:
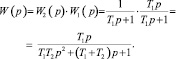(12)
Полученная передаточная функция ПФ второго порядка соответствует устойчивой системе, поскольку по Ляпунову для устойчивости линейной системы необходимо и достаточно, чтобы вещественные части корней характеристического уравнения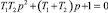 
были отрицательными, то есть лежали слева от мнимой оси плоскости корней. В нашем случае 
, 
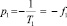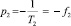. Поскольку f1,2 – частоты, которые всегда выражаются положительными и действительными числами, корни характеристического уравнения, описывающего уравнения свободного движения ПФ, всегда отрицательные и действительные числа.
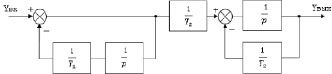
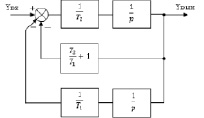
Существует множество вариантов схемной реализации ПФ. В данной работе для полученной в (12) передаточной функции были синтезированы две структурные схемы рекурсивных фильтров с бесконечной импульсной характеристикой (БИХ) [4], представленные на рис. 2. Первая схема (рис. 2, а) получена по формуле (7) как последовательное соединение фильтров высоких и низких частот. Вторая (рис. 2, б) – как реальное дифференцирующее звено второго порядка, соответствующее результирующей передаточной функции W(p).
Результаты исследования и их обсуждение
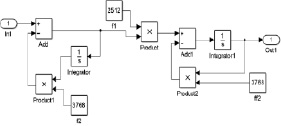
Апробация разработанных алгоритмов полосовой фильтрации была произведена в среде MATLAB. Структурные схемы моделей двух реализаций полосового фильтра в Simulink приведены на рис. 3, a, б.
Полученные амплитудно-частотные характеристики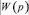 
(АЧХ) для двух реализаций ПФ, настроенных на полосу пропускания [f1 = 400 Гц; f2 = 600 Гц] (или для угловой частоты – [ω1 = 2512 рад/c; ω2 = 3768 рад/c]), представлены на рис. 4. Форма АЧХ фильтра далека от прямоугольной в связи с неидеальностью реализации фильтра, вносящей искажения в полосе пропускания и неидеально подавляющией сигнал в полосе заграждения.
a
б
Рис. 2. Структурные схемы реализаций полосового фильтра: a – первая реализация ПФ; б – вторая реализация ПФ
a
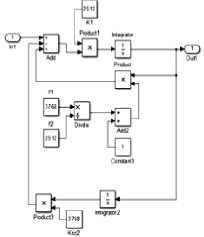
б
Рис. 3. Модель полосового фильтра в Simulink: a – первая реализация ПФ; б – вторая реализация ПФ
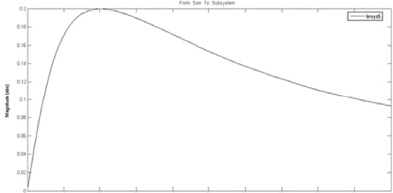
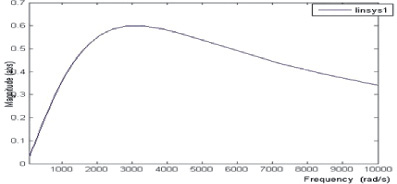
Рис. 4. Амплитудно-частотные характеристики (АЧХ) и затухание двух реализаций полосовых фильтров (верхний график – первая реализация, нижний график – вторая реализация)
Как показал эксперимент, первая реализация ПФ характеризуется худшим качеством АЧХ – максимальный коэффициент передачи в полосе пропускания 0,4, в то время как для второй реализации фильтра этот показатель равен 0,6. Это объясняется специфическими особенностями передающих свойств последовательных соединений звеньев и систем с множественными обратными связями, осуществляющими регулирование по отклонению. В этой связи для дальнейших исследований была выбрана вторая реализация ПФ (рис. 3, б и 4, б).
В ходе модельного эксперимента на вход ПФ подавался периодический несинусоидальный сигнал, имитирующий экспериментально полученную функцию изменения пульсаций давления в предпомпажном режиме (рис. 1) и представляющий суперпозицию гармонических составляющих различной частоты.
Спектры входного (верхний график) и выходного (нижний график) сигнала ПФ представлены на рис. 5. Основной пик пульсаций в предпомпажном режиме приходится на частоту f = 500 Гц, которая является центральной в выбранной полосе пропускания фильтра. Частота f = 200 Гц соответствует роторной частоте, амплитуда пульсаций при которой максимальна и равна ΔP = 0,1 кг/см2, в то время как выделяемой с помощью ПФ частоте f = 500 Гц соответствует вдвое меньшая амплитуда пульсаций ΔP = 0,05 кг/см2, что и обусловливает низкое качество фильтрации.
Выводы
Как показали результаты модельного экспериманта, применение алгоритмов полосовой фильтрации в составе САУ для идентификации предпомпажных режимов работы компрессора достаточно эффективно позволяет выявить появление пиков пульсаций давления, характеризующих приближение к границе устойчивости.
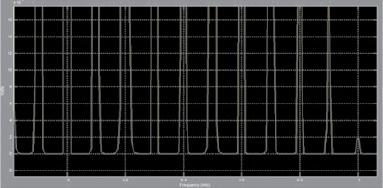
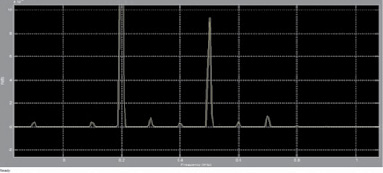
Рис. 5. Спектры входного и выходного сигнала ПФ
Использованный БИХ фильтр имеет более простую реализацию по сравнению с КИХ фильтрами.
Для улучшения качества ПФ возможно применение оконных sinc-фильтров (например, Хэмминга или Блэкмана), позволяющих увеличить амплитуду сигнала в полосе пропускания и затухание сигнала вне ее [6].