Проблема регулирования потоков транспортируемых сред различной природы, в том числе в трубопроводах, не теряет своей актуальности в первую очередь, благодаря интенсификации производственных линий за счет роста единичных мощностей составляющих их устройств в условиях повышенных требований к параметрам эксплуатации, контролю градиентов давлений, расходных характеристик и т.д. для указанных течений. Отметим, что в общем случае данные регулирующие органы функционально контролируют не только процесс регулирования расхода среды, но также перекрытия, разделения или смешивания ее потоков. К основным задачам проектирования регулирующих органов трубопроводов относится совершенствование инженерных методов их расчета для различных режимов течений дисперсных сред [4, 8, 13, 20, 39]. При этом предполагается проведение теоретико-экспериментальных исследований по оценке различных параметров, влияющих на работу трубопроводной арматуры. В частности, важной областью данных исследований является определение функциональных зависимостей двух основных видов – для пропускной σ(l) и расходной q(l) безразмерных характеристик регулирующих органов от степени их закрытия
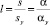
(или пропускной способности Kv(l), м3/ч, и безразмерного коэффициента расхода μпр(l)). Здесь s и sy – значения текущего и номинального полного хода затвора; α и αy – значения текущего и номинального полного угла поворота.
Цель работы: анализ современных способов оценки коэффициента гидравлического сопротивления при транспортировании однокомпонентных сред различной природы в регулирующих органах на основе известных литературных источников.
Об основных типах и назначении регулирующих органов
Согласно классическим монографиям [4, 8] и справочникам [13, 20, 39], в том числе посвященным гидравлическим регулирующим устройствам (при действии на затвор органа в консервативных условиях – за счет энергии рабочей среды, а не притока энергии извне), различают: регуляторы прямого действия (поддержание давления и уровня) [39]; клапаны – предохранительные [4] (сброс повышенных давлений) и обратные (защита от обратных протечек); поворотные заслонки [4, 8, 13, 20, 39]. Причем регуляторы прямого действия [39] или регулирующие клапаны [4] могут функционировать при подаче транспортируемой среды «на затвор (плунжер)» или «под затвор (плунжер)» в зависимости от того, на каком участке трубопровода требуется контроль давления – на входе или на выходе из этого устройства.
Обеспечение местного гидравлического сопротивления в потоке среды с целью управления ее расходом, перепадом давления и другими режимными параметрами относится к понятию дросселирования [8, 12]. Например, эффект дросселирования реализуется: в зазоре (щели) между двумя частями затвора (плунжера) – подвижной (золотником) и неподвижной (седлом) – при изменении степени закрытия сечения между ними (проходного сечения) и коэффициента гидравлического сопротивления; в узких трубках спирального профиля (винтовых дросселях) при возрастании сопротивления за счет инерционных потерь; при движении регулирующего элемента внутри или снаружи цилиндра с дроссельными отверстиями различной формы и т.д. [22].
В связи с этим конструктивно различают: односедельные, двухседельные, клеточные, мембранные и др. виды регулирующих клапанов [4, 8, 13, 20, 22, 39].
Основные виды гидродинамических характеристик регулирующих органов
Перечисленные типы клапанов характеризуются практически одним набором взаимосвязанных друг с другом гидродинамических параметров: расходом, перепадом давления Δp и коэффициентом гидравлического сопротивления ζ среды плотностью ρ, движущейся со средней скоростью течения w, в том числе с помощью выражений для объемного Q (или массового G) расхода и формулы Вейсбаха
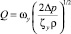 или
или 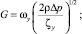 (1)
(1)
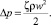 (2)
(2)
Считается, что среда проводит звук с местной скоростью a и обладает вязкостями – динамической μ и кинематической ν = μ/ρ; внутренние поверхности каналов имеют шероховатость с коэффициентом трения kэ. В частности, для односедельного или двухседельного органов к конструктивным параметрам относятся: характерные размеры – для прямолинейных участков L и проходов – дроссельного h, условного (номинального диаметра входного патрубка) Dy, гидравлического (диаметр проходного сечения) DΓ; площади сечений – для камер до и после расширения (сужения) потока ωкан1 и ωкан1; для каналов ωкан; проходного ωпр; условного прохода ωу; значения – углов для поворота потока φ и конусности насадка θ; радиуса скругления r и глубины фаски l′ входного отверстия.
С учетом влияния на транспортирование потока пристеночного трения, кавитационных эффектов, кинематического подобия в интервале времени T и шумового воздействия дополнительно вводятся в рассмотрение критерии Рейнольдса, Эйлера, Струхаля и Маха. Для анализа течений среды в регулирующих органах наряду с указанными ранее во введении функциями для пропускной σ(l) и расходной q(l) характеристик (согласно определениям 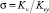 и
и 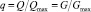 [4, 8, 13, 20, 39]), могут быть использованы функциональные зависимости: пропускной способности Kv; коэффициента гидравлического сопротивления для проходного сечения ζпр (или условного прохода ζy); коэффициента расхода среды – аналогично μпр (или μy) от указанных критериальных чисел
[4, 8, 13, 20, 39]), могут быть использованы функциональные зависимости: пропускной способности Kv; коэффициента гидравлического сопротивления для проходного сечения ζпр (или условного прохода ζy); коэффициента расхода среды – аналогично μпр (или μy) от указанных критериальных чисел
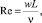
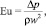
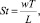
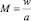
и безразмерных показателей, составленных из набора конструктивных параметров устройства.
О взаимосвязи гидродинамических характеристик регулирующих органов
Перечисленные выше характеристики Kv; ζпр (или ζy); μпр (или μy) также взаимосвязаны
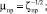
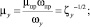 (3)
(3)
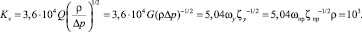 (4)
(4)
Заметим, что формула (4) соответствует определению пропускной способности Kv, как расхода воды (ρ = 103 кг/м3), пропускаемой регулирующим устройством при градиенте давления на нем 0,1 МПа. Кроме того, для гидравлических регулирующих органов типа клапанов (с дросселирующим эффектом) и поворотных заслонок обеспечиваются различные виды зависимости σ(l). В первом случае профилируется линейная и логарифмическая (равнопроцентная) пропускная характеристика с учетом начальных условий
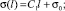
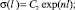
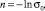 (5)
(5)
а во втором – профилирование отсутствует (σ(l) – нелинейная) относительно параметра 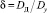 – отношения диаметров диска затвора и условного прохода при угле поворота заслонки α = (0° – 60°) [4]:
– отношения диаметров диска затвора и условного прохода при угле поворота заслонки α = (0° – 60°) [4]:
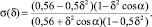 (6)
(6)
Итак, значимость совершенствования способов для оценки коэффициента гидравлического сопротивления транспортируемых сред в указанных устройствах подтверждается формулами взаимосвязи (1)–(4) для основных показателей процесса регулирования потоков. Наиболее развитые методы расчета гидравлических сопротивлений регулирующих органов относятся к области течений однокомпонентных жидкостей и газов.
Общий подход к оценке коэффициента гидравлического сопротивления проточной части при течениях однокомпонентных жидкостей
Заметим, что при расчете гидравлического сопротивления используется метод суперпозиции местных потерь давления [3, 4, 8–10, 13, 20, 39] вследствие сложной геометрии проточных частей регулирующих органов для трубопроводов. Вопросы истории теории гидравлического удара в самой трубе отражены в работе [2].
Разбивая проточную часть регулирующего органа на характерные участки, соответствующие потерям давления в местных сопротивлениях (например, в прямых каналах, при повороте потоков, сжатии сечений, внезапном расширении, слиянии течений и т.д.), согласно формуле Ж. Борда
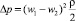 (7)
(7)
моделируется суммарный перепад давления, а следовательно, и функция полного гидравлического сопротивления ζy = ζy(ε) от коэффициента сжатия струи ε.
При этом решаются частные случаи классической задачи Н.Е. Жуковского о сжатии жидкостной среды при ее выходе через плоскую щель в сосуде конечной ширины и бесконечной длины [3, 4, 8, 10], когда транспортируемая среда движется со скоростями w1, wсж, w2 – в зонах с начальным «1», суженным (щелевым) «3» и широким «2» сечениями ω1, ω3, ω2 [12]. Теоретические исследования изменения формы струи идеальной жидкости при ее истечении из щели в различных условиях не теряют актуальности, в частности из дна резервуара [1], при наличии точечного источника [36]. Коэффициент сжатия струи ε = ε(n) для транспортируемой среды является функцией от параметра n = ω3/ω1 – степени сжатия потока. Однако для практических приложений требуется, как правило, по ограниченным экспериментальным данным оценить целесообразность применения того или иного регулирующего устройства [9, 10], что бывает затруднительно сделать, пользуясь только аналитическими громоздкими методиками. В таких случаях применяются эмпирические или полуэмпирические формулы, стандартные способы. Причем те из них, которые многократно апробированы, содержатся в соответствующих нормативных источниках, например [35]. Справочная литература [3–5, 8, 13, 20, 33, 38, 39] обобщает результаты соответствующих теоретико-экспериментальных исследований и служит руководством для выбора регулирующего органа, предназначенного реализовать помимо регулирования расхода рабочей среды заданный технологический процесс перекрытия, разделения или смешивания ее потоков.
Таким образом, формируются схемы расчета для простых местных сопротивлений на отдельных геометрических участках течений однокомпонентных жидкостных сред согласно (7) с учетом вида ε = ε(n) и режима потока. Режимы движения жидкости через регулирующий клапан разделяются на ламинарный, переходный и турбулентный, в частности согласно [4] данные области могут соответствовать диапазонам: Re ≤ 10; 10 < Re < 104; Re ≥ 104. Заметим, что наибольшие сложности вызывает расчет гидродинамического сопротивления для второго из перечисленных случаев вследствие требующей уточнения зависимости ε от числа Re и эквивалента шероховатости kэ внутренних поверхностей проточных частей регулирующих устройств. В зоне ламинарного течения жидкости наблюдается обратная пропорциональность коэффициента ζ критерию Рейнольдса [3], а в турбулентной зоне – предложенные формулы для ζ не содержат число Re [4, 8, 13, 20, 39].
Примеры расчета гидравлического сопротивления проточной части при течениях однокомпонентных жидкостей
Например, в работах [3, 4, 8] различными авторами анализируются полученные для турбулентных течений указанных жидкостных сред полуэмпирические апробированные формулы вида ε = ε(n) для различных форм плоских щелей (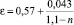 – А.Д. Альтшуль; ε = 0611 + 0,148n2 – В.В. Ведерников;
– А.Д. Альтшуль; ε = 0611 + 0,148n2 – В.В. Ведерников; 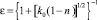 – К.В. Химицкий, где коэффициент k0 учитывает геометрию щели и др.). При Re ≥ 104 (в квадратичной области сопротивления)
– К.В. Химицкий, где коэффициент k0 учитывает геометрию щели и др.). При Re ≥ 104 (в квадратичной области сопротивления) 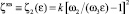 [3], т.е. предлагается пренебречь потерями давления на сжатие и ограничиться оценкой искомого показателя при внезапном изменении сечения потока, введя поправочный коэффициент k, который учитывает неоднородность распределения скоростей по сечению, вязкость и др. эффекты. При Re < 3,2 (в ламинарной области сопротивления, когда n = 1) исследуется движение жидкости через различные насадки: круглое сечение в диафрагме трубы ζлм = 25,2/Re – В. Вюст [3]; трубу Вентури с углом конусности θ, когда
[3], т.е. предлагается пренебречь потерями давления на сжатие и ограничиться оценкой искомого показателя при внезапном изменении сечения потока, введя поправочный коэффициент k, который учитывает неоднородность распределения скоростей по сечению, вязкость и др. эффекты. При Re < 3,2 (в ламинарной области сопротивления, когда n = 1) исследуется движение жидкости через различные насадки: круглое сечение в диафрагме трубы ζлм = 25,2/Re – В. Вюст [3]; трубу Вентури с углом конусности θ, когда
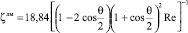
[4, 38] и т.д. В переходной режимной зоне предлагается применить принцип суперпозиции потерь давления, когда выполняется равенство ζпер = ζлм + ζлм [4, 3]. В частности, согласно [5] искомые показатели при 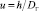 для односедельного регулирующего клапана (1,7 ≤ u ≤ 30) равны
для односедельного регулирующего клапана (1,7 ≤ u ≤ 30) равны
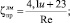 Re ≤ 10;
Re ≤ 10;
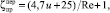 10 < Re < 104;
10 < Re < 104;
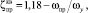 Re ≥ 104.
Re ≥ 104.
Ставшие уже классическими основные подходы [3–5, 8, 13, 20, 33, 38, 39] к расчету гидравлических сопротивлений регулирующих органов при транспортировании однокомпонентных жидкостей, несмотря на свое разнообразие, уточняются и расширяются вследствие постоянно возрастающих требований к энергоэффективности соответствующего арматурного оборудования.
В работе [24] для турбулентной зоны клапанного узла по типу трубы Вентури получена эмпирическая зависимость вида
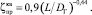
Сравнение указанных результатов [24] и расчетов для диафрагм с утолщенными краями в соответствии с методикой [20] позволило выявить диапазон применимости последней формулы: 0,75 ≤ L/DΓ ≤ 2,25.
Для практических приложений представляет особый интерес подход, описанный в работе [10] для бескризисного турбулентного режима течения жидкости в трубе Вентури, когда в качестве основных характеристик выбраны: ζ1с,с – коэффициент гидравлического сопротивления для входного участка до сжатия струи (в сечении «c-c», аналогичного ранее введенному сечению ω3), отнесенный к скорости wc ≡ wсж; 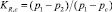 – степень «восстановления» давления в указанном сжатом сечении. Здесь: p1, pc ≡ p3, p2 – давления среды во входном «1», суженном (щелевом) «3» и выходном «2» сечениях ω1, ω3, ω2. Дадим определения параметрам, отличным от введенных ранее:
– степень «восстановления» давления в указанном сжатом сечении. Здесь: p1, pc ≡ p3, p2 – давления среды во входном «1», суженном (щелевом) «3» и выходном «2» сечениях ω1, ω3, ω2. Дадим определения параметрам, отличным от введенных ранее: 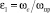 – коэффициент сжатия струи по отношению к лимитирующему проходному сечению ωпр;
– коэффициент сжатия струи по отношению к лимитирующему проходному сечению ωпр; 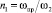 – степень сужения струи по отношению к выходному сечению ω2; ζ12,2 – коэффициент гидродинамического сопротивления между сечениями ω1 и ω2, отнесенный к выходной скорости потока w2. Учитывая связь между ζ12,2 и μ12,пр – коэффициентом расхода жидкости в форме
– степень сужения струи по отношению к выходному сечению ω2; ζ12,2 – коэффициент гидродинамического сопротивления между сечениями ω1 и ω2, отнесенный к выходной скорости потока w2. Учитывая связь между ζ12,2 и μ12,пр – коэффициентом расхода жидкости в форме 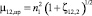 [8], согласно принципам суперпозиции потерь давления в соответствии с формулой (7) и максимального расхода в работе [10] получено следующее соотношение:
[8], согласно принципам суперпозиции потерь давления в соответствии с формулой (7) и максимального расхода в работе [10] получено следующее соотношение:
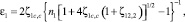 (8)
(8)
где параметры потока в сжатом сечении «c-c» могут быть найдены по предложенным двум методикам на базе уравнения импульсов или уравнения Бернулли при равенстве давлений в проходном и сжатом сечениях. Описанный подход к оценке ζ1с,с и KR,c применяется в работе [9] для расчета предельного коэффициента расхода для оптимальной проточной части насадки Вентури.
В случае исследования воздействия потока жидкости на затворы различных форм (конической, шаровой, вогнутой) в регуляторе прямого действия [6] выявлена аналогия с дросселированием течений в диафрагме. При этом характер падения давления на фронтальную часть от штока к кольцевой щели определяется геометрией затвора и его ходом. В работах [6, 7] получена эмпирическая формула для коэффициента гидравлического сопротивления в форме экспоненциальной зависимости
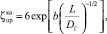
где опытный параметр b, учитывающий форму затвора, меняется в диапазоне 0,62 ≤ b ≤ 1. Анализ экспериментальных исследований гидравлических сопротивлений для однотрубных систем отопления с запорно-регулирующей арматурой в зависимости от степени ее регулирующего органа, в частности, на примере работы трехходового термостатического клапана, проведен в работе [11]. Кроме того, при проектировании шиберных задвижек применяется полуэмпирическая зависимость вида ε = 0,62 + 0,38n2 для расчета коэффициента гидравлического сопротивления с помощью выражения
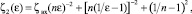
где n – отношение проходного сечения к площади сечения трубы; ζвх – значение ζ при входе жидкости в зазор [37, 40].
О взаимосвязи коэффициента гидравлического сопротивления и расходных характеристик при течении сжимаемых сред
Сопоставление формул: Вейсбаха (2) для потери давления Δρ на гидравлических сопротивлениях и Дарси – Вейсбаха для потери энергии dhT на преодоление гидравлических сопротивлений по длине Δh трубы при ее приращении dx в случае течения газа вне критических скоростей [4, 8, 13, 20, 39]
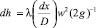 (9)
(9)
приводит к условному выражению коэффициента гидравлического сопротивления ζy (через эквивалентную этому сопротивлению длину трубы lэк) в форме параметра Дарси
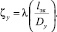 (10)
(10)
Здесь λ – коэффициент потерь на трение по длине трубы lэк; Dу – условный (номинальный) диаметр входного патрубка регулирующего органа, равный диаметру выходного. Обозначим соответственно давления на входе и выходе p1 и p1.
Ограничимся случаем докритических скоростей течений газа или пара в дроссельном проходе регулирующего устройства, например, когда согласно [4] 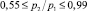 , если при
, если при 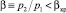 не достигается максимальная скорость потока, равная скорости звука в сжимаемой среде при транспортировании через данное устройство. Показатель ζy используется для оценки массового расхода газа в регулирующем органе, например
не достигается максимальная скорость потока, равная скорости звука в сжимаемой среде при транспортировании через данное устройство. Показатель ζy используется для оценки массового расхода газа в регулирующем органе, например
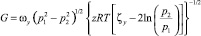 ,
,
где ωy – сечение условного прохода; z – опытный коэффициент сжимаемости неидеального газа; R – универсальная газовая постоянная; T – абсолютная температура. Заметим, что для течения пара последнее выражение принимает вид
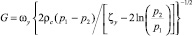
при усредненном значении плотности среды ρc [4, 20, 8]. Дополнительные сложности расчетов расходных характеристик связаны с учетом состояния пара (перегретого, насыщенного, влажного), каждое из которых может реализовываться в процессе дросселирования. При этом показатель адиабаты уточняется в соответствии с таблицами термодинамических свойств водяного пара.
Например, работа [17] посвящена полуэмпирическому методу построения расходных характеристик дроссельно-регулирующей арматуры, в частности анализу зависимости 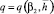 в виде уравнения эллипса
в виде уравнения эллипса
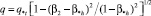
для клапанов: тарельчатого с диффузорным седлом и профилированного с конфузорным седлом. Здесь: 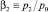 – отношение давлений пара за клапаном p2 и при полном его торможении p0;
– отношение давлений пара за клапаном p2 и при полном его торможении p0; 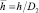 – отношение высоты подъема клапана h к диаметру узкого сечения седла D2; q*t – отношение критических расходов через клапан соответственно при произвольном и максимальном (при полном открытии) значениях h; β*h – значение β2 при достижении критического расхода среды для произвольного значения относительного подъема клапана
– отношение высоты подъема клапана h к диаметру узкого сечения седла D2; q*t – отношение критических расходов через клапан соответственно при произвольном и максимальном (при полном открытии) значениях h; β*h – значение β2 при достижении критического расхода среды для произвольного значения относительного подъема клапана  . Заметим, что при малых значениях h профилированный клапан соответствует осесимметричному кольцевому соплу Лаваля с высокой степенью расширения, а при стремлении h к полному открытию – профилю суживающего сопла [23].
. Заметим, что при малых значениях h профилированный клапан соответствует осесимметричному кольцевому соплу Лаваля с высокой степенью расширения, а при стремлении h к полному открытию – профилю суживающего сопла [23].
Заметим, что в критическом случае течений сжимаемых сред 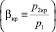 , при условии достижения максимального значения их массового расхода связь между ζy и βкр определяется выражением
, при условии достижения максимального значения их массового расхода связь между ζy и βкр определяется выражением 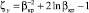 [33]. Например, для двухатомного газа при адиабатическом процессе параметр адиабаты k = 1,4 и βкр = 0,528, для перегретого водяного пара соответственно k = 1,3 и βкр = 0,546 [35]. Оценка коэффициента сжатия струи газа при истечении через диафрагмы, щели, насадки Борда с острыми входными кромками при сверхкритических перепадах давления в отверстии исследована в работе [34]. Заметим, что равномерный профиль скорости потока в сужающемся канале предполагает достижение ее критического значения при
[33]. Например, для двухатомного газа при адиабатическом процессе параметр адиабаты k = 1,4 и βкр = 0,528, для перегретого водяного пара соответственно k = 1,3 и βкр = 0,546 [35]. Оценка коэффициента сжатия струи газа при истечении через диафрагмы, щели, насадки Борда с острыми входными кромками при сверхкритических перепадах давления в отверстии исследована в работе [34]. Заметим, что равномерный профиль скорости потока в сужающемся канале предполагает достижение ее критического значения при 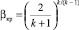 [14, 15], а для узкого сечения сопла Лаваля принимается
[14, 15], а для узкого сечения сопла Лаваля принимается 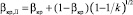 [14, 16]. Необходимость расширения области обтекания потоками пара перфорированной поверхности в регулирующих профилированных клапанах при сверхкритических перепадах давления обсуждается в работе [16] на примере сравнения результатов исследований работы тарельчатого и профилированного регулирующих устройств паровых турбин.
[14, 16]. Необходимость расширения области обтекания потоками пара перфорированной поверхности в регулирующих профилированных клапанах при сверхкритических перепадах давления обсуждается в работе [16] на примере сравнения результатов исследований работы тарельчатого и профилированного регулирующих устройств паровых турбин.
Способы расчета гидравлического сопротивления проточной части с интенсивным дросселированием при течениях сред различной природы
С целью интенсификации процесса дросселирования в проточных частях регулирующих органов применяются различного рода разгруженные регулирующие элементы, например с многоступенчатым рядом решеток, со сквозными отверстиями (как в подвижной, так и в неподвижной частях данного элемента), в том числе с возможным поворотом золотника относительно гильзы при образовании проходного сечения их взаимно ответными отверстиями и т.п. Выбор оптимального способа дросселирования в проточной части арматурного устройства определяется обеспечением наименьших значений коэффициента гидравлического сопротивления и степени шумовых эффектов.
В работе [21] введен геометрический фактор идентификации
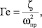
где ωпр – проходное сечение. Условие равенства параметра Γe для заданных (требуемых) показателей процесса дросселирования и для геометрии проточной части конкретного устройства может служить критерием выбора способа интенсификации для регулирования потоков транспортируемой среды. Предложена схема исследования характера для изменения коэффициента гидравлического сопротивления с учетом потерь давления рабочего потока в дополнительных регулирующих элементах 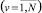 проточной части арматурного устройства. В частности, расчет производится согласно выражениям
проточной части арматурного устройства. В частности, расчет производится согласно выражениям
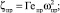
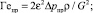
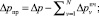
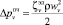 [21].
[21].
Отметим, что вопросы получения уравнений для гидравлического сопротивления актуальны и в случае проектирования клапанных тарелок, в частности, с перекрестно-прямоточным движением фаз рабочей среды [28].
Сложная геометрия проточной части регулирующих органов является предпосылкой для применения метода компьютерного моделирования процесса дросселирования потоков рабочих сред. Гидравлические расчеты в среде трехмерного CFD модуля ANSYS Fluid, выполненные в работах [25–27], позволили модернизировать промышленный клапан дискового типа, применив дроссельную решетку. В других работах [30, 31] с помощью стандартной (k – ε)-модели турбулентного течения исследовано применение перфорированной направляющей затвора (или его седла) для получения течений направленных друг против друга струй во внутреннюю полость указанной клетки в осесимметричных клапанах. Последние имеют надежную пропускную способность при достаточно малых габаритах. На примере потоков капельных жидкостей и газов при температуре до 180 °C и давлении до 16 МПа в трубопроводах при выборе оправданного минимального значения коэффициента гидростатического сопротивления
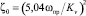
численно анализируется соотношение между диаметрами R/r – внутренним R для сепаратора и для отверстий в нем r. В частности, достижение значений ζ0 = 1,5 обеспечивается R/r ≥ 20 и шагом размещения отверстий в сепараторе H > 4; ζ0 = 2,0 соответственно R/r ≥ 26 и 1,3 ≤ H ≤ 1,5 [30, 31]. В работе [29] анализируются результаты численного эксперимента, заменяющего натурные опытные испытания, по выбору размера сетки в дросселирующем распределителе при течении рабочих жидкостей. Построенные в этом случае твердотельные компьютерные модели проточной части пары гильза-золотник используются при разработке рекомендаций по расположению дроссельных щелей при заданных характеристиках гидроэлементов. Вопросы компьютерного моделирования в среде Matlab для операции регулирования шума в пневматических и газотранспортных системах с помощью глушителей, расположенных за регулирующими органами (например, при установлении дроссельной шайбы), для обеспечения санитарных и прочностных нормативов освещаются в работах [18, 19]. Сравнение результатов для трехмерных компьютерных моделей движения потоков пара при температурном режиме до 650 °C в регулирующих клапанах [41], в том числе с параболическим конусом и цилиндром с отверстиями, показало предпочтительное использование последних вследствие более равномерного распределения рабочей среды в проточной части устройства.
Заключение
Таким образом, проблема расчета гидравлического сопротивления регулирующих органов при транспортировании однокомпонентных сред не теряет своей актуальности, несмотря на наличие классических способов оценки гидродинамических характеристик. Данное обстоятельство объясняется широким применением регулирующих устройств для указанных целей и возрастающей потребностью соответствовать требованиям энергосбережения при эксплуатации арматурного оборудования. Особенно развитыми с точки зрения наличия адаптированных аналитических и полуэмпирических выражений являются методики расчета гидравлического сопротивления проточной части при течениях однокомпонентных жидкостей, постоянно развивающимися – для потоков сжимаемых сред. Однако наличие их критических режимов при транспортировании через регулирующие органы приводит к необходимости борьбы с нежелательными эффектами, препятствующими энергосбережению различного рода ресурсов, что отражается на задачах совершенствования, модернизации существующих процессов регулирования потоков рабочих сред с совмещением с другими операциями – смешиванием, разделением, перекрытием их потоков, а также разработке новых инженерных методов расчета регулирующих органов целевого назначения. Одним из способов решения указанных задач является создание гидравлического сопротивления проточной части с интенсивным дросселированием при течениях сред различной природы.



