В современном развитом государстве при управлении экономикой большое значение имеет применение прогнозирования как метода, способного регулировать развитие общества на ближайшие несколько лет или даже десятилетий. В условиях перехода к рыночным отношениям прогнозирование приобретает весьма большое значение и становится начальной стадией, основой всей системы управления. Это связано с тем, что в условиях рынка меняются траектории развития, увеличивается выбор его вариантов, усиливается интенсивность поиска выходов из нежелательных, негативных ситуаций. Достигается это с помощью развитой системы альтернативных прогнозов. Прогнозирование социально-экономического развития представляет собой систему научных исследований количественного и качественного характера, направленных на выявление тенденции развития национального хозяйства или его частей. Оно является прикладным исследованием, которое проводится для получения новой информации, полезной для управления экономическим развитием. В теории и практике прогнозирования накоплен значительный набор различных методов, которых более сотни. Но, как считают некоторые ученые, на практике используются лишь 15–20 методов [7].
Методы прогнозирования непрерывно обогащаются и совершенствуются. В экономической литературе представлено их большое разнообразие. Так, исследователи [3] говорят, что все многообразие методов прогнозирования основано на двух подходах – эвристическом и математическом. Эвристические методы базируются на использовании явлений или процессов, не поддающихся формализации. Среди математических методов в особую группу выделяются методы анализа и прогнозирования динамики экономических процессов, которые реализуются средствами современной вычислительной техники [3].
Учитывая тот факт, что экономические условия развития предприятия, отрасли, страны изменяются во времени, необходимо анализировать динамику этих изменений для успешной реализации функций управления. Одним из приемов, которым целесообразно воспользоваться при оценке эффективности будущих управленческих решений, являются методы прогнозирования, основанные на анализе временных рядов, цель которых – предсказать с той или иной степенью надежности будущие события и учесть этот прогноз при планировании тех или иных управленческих решений [5]. В отечественной литературе можно встретить множество работ, посвященных прогнозированию экономических показателей развития регионов и страны в целом [1, 2, 4, 6, 8].
Учитывая актуальность проблемы, авторы определили цель исследования – анализ и прогнозирование динамики уровня безработицы в России, декомпозиция временного ряда и проведение прогнозных расчетов.
1. Тренд-сезонный анализ временного ряда уровня безработицы в России
Показатели временного ряда уровня безработицы в России за период с 2002 по 2014 год приведены в табл. 1.
В целях анализа и прогнозирования временного ряда нами решены следующие задачи:
– анализ тренда (позволяет отфильтровать шум и периодические колебания, преобразуя данные в относительно гладкую кривую, для выявления тенденции ряда и прогноза его будущих значений);
– декомпозиция временного ряда (позволяет выделить в ряде тренд, сезонную, циклическую и случайную составляющую для проведения его структурного анализа);
– автокорреляционный анализ (позволяет определить периодические компоненты ряда).
Экономические процессы чаще всего имеют многокомпонентную структуру (3)
yt = lt + st + vt + ut, (1)
где lt – тренд, представляющий собой ход кривой, со спокойным гладким характером, которая описывает долговременные изменения и определяет главное направление развития; st – сезонная компонента, кратковременные регулярные колебания; vt – циклическая компонента, долгосрочные регулярные колебания; ut – случайная составляющая временного ряда, отражающая воздействие многочисленных факторов случайного характера.
Функции тренда для одномерных временных рядов могут представляться полиномами различных степеней и другими функциями относительно переменной времени t = 1, 2, …, n (моделями кривых роста).
Для автоматизации расчетов по анализу и прогнозированию временных рядов нами в работе использовано программное средство Gretl 1.7.1. Результатом построения полиномиального тренда уровня безработицы (U_B) явилась модель линейного вида:
u_bt = 8,58 – 0,02t. (2)
Модель адекватна, параметры значимы (по t-критерию Стьюдента) на уровне 1 %, скорректированный коэффициент детерминации 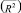 равен 0,55. В пользу линейной формы тренда говорит еще и высокий коэффициент автокорреляции первого порядка (0,95).
равен 0,55. В пользу линейной формы тренда говорит еще и высокий коэффициент автокорреляции первого порядка (0,95).
Таблица 1
Динамика уровня безработицы в России за 2002–2014 гг. (в % на конец месяца)
|
2002 |
2003 |
2004 |
2005 |
2006 |
2007 |
2008 |
2009 |
2010 |
2011 |
2012 |
2013 |
2014 |
|
|
Январь |
8,6 |
9,3 |
9,1 |
8,3 |
7,7 |
7,1 |
6,6 |
8,7 |
9,0 |
7,6 |
6,3 |
6,0 |
5,6 |
|
Февраль |
8,4 |
9,6 |
9,5 |
8,3 |
7,9 |
7,2 |
7,1 |
9,4 |
8,5 |
7,4 |
6,2 |
5,8 |
5,6 |
|
Март |
8,3 |
9,2 |
8,9 |
8,0 |
7,8 |
6,8 |
6,5 |
9,2 |
8,5 |
7,0 |
6,3 |
5,7 |
5,4 |
|
Апрель |
8,3 |
8,8 |
8,2 |
7,6 |
7,6 |
6,4 |
6,0 |
8,8 |
8,1 |
7,1 |
5,6 |
5,6 |
5,3 |
|
Май |
8,2 |
8,5 |
7,6 |
7,3 |
7,5 |
5,9 |
5,4 |
8,5 |
7,2 |
6,2 |
5,2 |
5,2 |
4,9 |
|
Июнь |
7,5 |
8,4 |
7,5 |
7,3 |
7,2 |
5,8 |
5,6 |
8,3 |
6,7 |
6,0 |
5,2 |
5,4 |
4,9 |
|
Июль |
7,3 |
8,3 |
7,4 |
7,2 |
6,9 |
5,7 |
5,7 |
8,1 |
6,8 |
6,4 |
5,2 |
5,3 |
4,9 |
|
Август |
7,1 |
8,2 |
7,3 |
7,1 |
6,5 |
5,6 |
5,8 |
7,9 |
6,7 |
6,0 |
5,0 |
5,2 |
4,8 |
|
Сентябрь |
7,6 |
8,2 |
7,7 |
7,2 |
6,6 |
5,6 |
6,2 |
7,6 |
6,5 |
6,0 |
5,0 |
5,3 |
4,9 |
|
Октябрь |
8,1 |
8,2 |
8,0 |
7,3 |
6,7 |
5,6 |
6,6 |
7,7 |
6,7 |
6,2 |
5,1 |
5,5 |
5,1 |
|
Ноябрь |
8,5 |
8,2 |
8,4 |
7,5 |
6,7 |
5,7 |
7,0 |
8,2 |
6,6 |
6,2 |
5,2 |
5,4 |
5,2 |
|
декабрь |
8,8 |
8,6 |
8,3 |
7,7 |
6,9 |
6,1 |
7,8 |
8,2 |
7,0 |
6,0 |
5,1 |
5,6 |
5,3 |
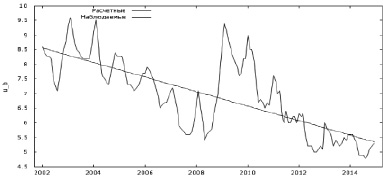
Рис. 1. Фактические данные и график линейного тренда уровня безработицы
Из визуального анализа графика (рис. 1) можно сделать вывод, что исходные данные представляют собой нестационарный временной ряд с выраженной цикличностью данных: ряд имеет тенденцию (непостоянное среднее), непостоянную дисперсию, существенные периодические колебания.
2. Прогнозирование по линейной модели уровня безработицы в России на 2015–2017 гг.
Учитывая хорошие свойства построенной линейной модели, можно сделать прогнозные расчеты. Результаты прогнозирования уровня безработицы на 2015–2016 гг. представлены в табл. 2.
Таблица 2
Результаты прогнозирования временного ряда уровня безработицы
|
Наблюдение |
Прогноз |
Стандартная ошибка |
Доверительный интервал |
|
2015 (январь) |
5,3 |
0,87 |
3,6–7,0 |
|
2015 (февраль) |
5,3 |
0,87 |
3,6–7,0 |
|
2015 (март) |
5,3 |
0,87 |
3,6–7,0 |
|
2015 (апрель) |
5,3 |
0,87 |
3,5–7,0 |
|
2015 (май) |
5,2 |
0,87 |
3,5–7,0 |
|
2015 (июнь) |
5,2 |
0,87 |
3,5–6,9 |
|
2015 (июль) |
5,2 |
0,87 |
3,5–6,9 |
|
2015 (август) |
5,2 |
0,87 |
3,5–6,9 |
|
2015 (сентябрь) |
5,2 |
0,87 |
3,4–6,9 |
|
2015 (октябрь) |
5,1 |
0,87 |
3,4–6,9 |
|
2015 (ноябрь) |
5,1 |
0,87 |
3,4–6,8 |
|
2015 (декабрь) |
5,1 |
0,87 |
3,4–6,8 |
|
2016 (январь) |
5,1 |
0,87 |
3,4–6,8 |
|
2016 (февраль) |
5,1 |
0,87 |
3,3–6,8 |
|
2016 (март) |
5,0 |
0,87 |
3,3–6,8 |
|
2016 (апрель) |
5,0 |
0,87 |
3,3–6,7 |
|
2016 (май) |
5,0 |
0,87 |
3,3–6,7 |
|
2016 (июнь) |
5,0 |
0,87 |
3,2–6,7 |
|
2016 (июль) |
5,0 |
0,88 |
3,2–6,7 |
|
2016 (август) |
4,9 |
0,88 |
3,2–6,7 |
|
2016 (сентябрь) |
4,9 |
0,88 |
3,2–6,6 |
|
2016 (октябрь) |
4,9 |
0,88 |
3,2–6,6 |
|
2016 (ноябрь) |
4,9 |
0,88 |
3,1–6,6 |
|
2016 (декабрь) |
4,9 |
0,88 |
3,1–6,6 |
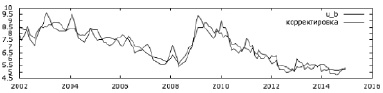
Рис. 2. Графики исходного и сезонно скорректированного ряда уровня безработицы
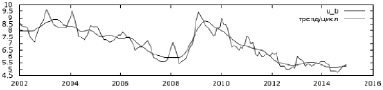
Рис. 3. Графики исходного ряда и тренд-циклической компоненты
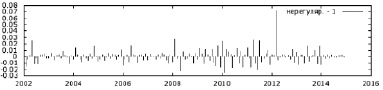
Рис. 4. График случайной составляющей временного ряда уровня безработицы
Проведём декомпозицию временного ряда значений уровня безработицы в России для:
– исключения влияния сезонной компоненты st, т.е. получения модифицированного сезонно скорректированного ряда;
– определения сезонной компоненты st и её прогноза;
– получения тренд-циклической компоненты ряда (lt + vt);
– выделения случайной составляющей временного ряда ut;
– структурного анализа ряда в целом.
На рис. 2, 3, 4 представлены результаты применения процедуры X-12-ARIMA и их графическое отображение.
Заключение
По результатам проведенной декомпозиции временного ряда значений уровня безработицы в России можно сделать следующие выводы:
1. Тренд-циклическая компонента оказывает существенное влияние на формирование уровней ряда, который демонстрирует циклическое поведение. Можно выделить цикл с 6-летним периодом, где пики безработицы приходятся на 2003 и 2009 годы, а спад на 2014 год.
2. Временной ряд также существенно подвержен эффекту сезонности, который проявляется с периодом в один год. Сезонная компонента имеет наибольшие значения и оказывает наибольшее влияние на формирование уровней ряда в декабре, январе, феврале, марте и апреле, т.е. на увеличение уровня безработицы в данный период. Наименьшее влияние данный фактор оказывает в мае, июне, июле, августе, сентябре, октябре и ноябре. Данные сезонные эффекты могут отчасти объясняться привлечением дополнительных кадров для выполнения сезонных работ.
3. Влияние случайной составляющей (различных несистематических факторов) несущественно – максимальное значение составило 0,07 в 2012 году.
Проведем дальнейший анализ выявленной сезонности ряда значений уровня безработицы, используя метод коррелограммы. Нами были оценены функции автокорреляции (ACF) и частной автокорреляции (PACF) с указанием значения максимального периода запаздывания (лага), который не должен превышать 15–20 % длины ряда. Оценочные результаты для ряда значений уровня безработицы в России, представленные на рис. 5, показывают чистую зависимость между наблюдениями ряда, разнесёнными на 1, 2, 6, 12 и 13 периодов, что позволяет оценить порядок запаздывания процесса n для модели авторегрессии AR(n) = AR(13).
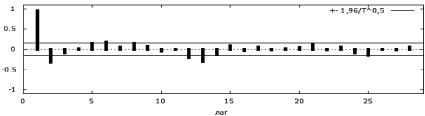
Рис. 5. График зависимости значений частной автокорреляционной (PАСF) функции от величины лага
Тест значимости коэффициента автокорреляции, называемый тестом Квенилле (Quenouille), свидетельствует, что если оцениваемый расчётный коэффициент больше критического значения ±1,96/Т0,5 (Т – число наблюдений ряда), то присутствует существенная зависимость между процессами для соответствующего лага (запаздывания между процессами). На коррелограмме горизонтальной линией отмечается граница доверительного интервала стандартной погрешности этого коэффициента. За пределы данной границы выходят 1, 2, 6, 12 и 13 значения частной автокорреляционной функции (PACF) (рис. 5).
Следовательно, можно сделать вывод о зависимости каждого значения ряда от предыдущего (лаг равен 1), от предшествующего предыдущему (лаг равен 2), от значения с периодом лага в 6 месяцев (лаг равен 6) а также от значения одноимённого месяца прошлого года (лаг равен 12) и предшествующего ему (лаг равен 13). Таким образом, существует сезонная составляющая в рассматриваемом ряду данных с длиной цикла 12 месяцев. Например, значение ряда в марте зависит от значения ряда в феврале (1), в январе (2), в июне (6) этого года, а также от значений ряда в марте (12) и феврале (13) прошлого года. Аналогичная зависимость имеет место для каждого значения ряда.
Рецензенты:
Адамадзиев К.Р., д.т.н., профессор, ФГБОУ ВПО «Дагестанский государственный университет», г. Махачкала;
Саркаров Т.Э., д.т.н., профессор, ФГБОУ ВПО «Дагестанский государственный технический университет», г. Махачкала.



