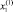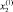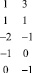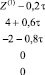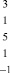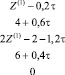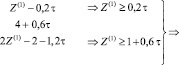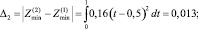В работе [1] показано, как на основе метода последовательного исключения переменных в системе линейных неравенств [2, 3] можно находить точное аналитическое решение задачи линейного программирования, коэффициенты которой зависят от параметра. Однако даже в случае однопараметрической задачи с двумя переменными [1] решение может оказаться громоздким. В практических же задачах линейного программирования коэффициенты обычно незначительно изменяются относительно своих средних значений, как, например, стоимость товара в зависимости от курса валют или инфляции. В подобных случаях, когда относительные изменения коэффициентов порядка 10 % и меньше, удобно использовать широко применяемый в различных исследованиях асимптотический метод возмущений [4, 5]. Суть его сводится к поиску разложения искомых функций в функциональные ряды, быстрота сходимости которых зависит от «параметра малости» – относительного изменения функций, влияющих на задачу.
Итерационная схема решения
Рассмотрим в общем случае задачу на минимум, преобразованную к системе линейных неравенств [3]:
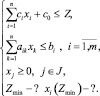(1)
В задаче на максимум в первом неравенстве (1) следует поменять знак «≤» на «≥» [3].
Обозначим через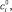 
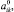
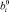средние значения всех коэффициентов:
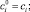
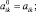
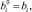
где, например, для непрерывных коэффициентов, зависящих от параметра t ∈ [0;1],
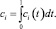(2)
Пусть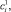 
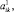
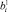означают отклонения этих коэффициентов от их средних значений:
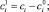
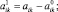
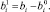
Тогда средние значения отклонений равны нулю:
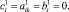(3)
Далее предполагается, что все относительные отклонения, например,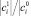 
, достаточно малы (менее 10 %).
Будем искать Z и xi для системы (1) в виде рядов, состоящих из поправок соответствующего порядка:
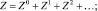
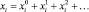(4)
Здесь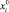 
и Z0 – решения (1), когда все коэффициенты равны своим средним значениям:
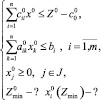(5)
Для нахождения поправок первого порядка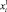 
и Z1 подставляем в (1):
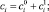
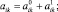
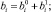
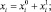
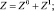
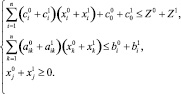
После раскрытия скобок получим
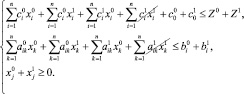
Относительные изменения первых поправок порядка относительного изменения коэффициентов. Зачёркнутые же слагаемые имеют второй порядок малости и поэтому должны быть отброшены [4]. Обозначим
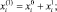
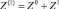
– решение в первом приближении теории возмущений. Тогда последняя система неравенств перепишется в виде
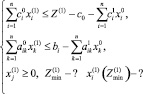(6)
У систем (5) и (6) одинаковые и постоянные коэффициенты при неизвестных. Отличаются только свободные члены. Поэтому обе системы решаются одинаково просто методом исключения [2, 3].
Для нахождения решения во втором приближении
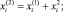
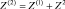
подставляем эти суммы вместо xi и Z в (1). После отбрасывания слагаемых третьего порядка малости получим
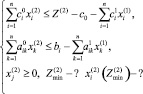(7)
Результаты (6), (7) нетрудно обобщить на любой порядок приближения р = 1, 2, …:
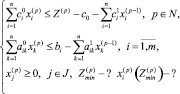(8)
Следует только иметь в виду, что при достаточно больших р асимптотические ряды начинают расходиться [5]. Критерием возможности увеличения р может, например, служить среднее отклонение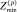 
от 
:
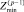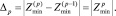(9)
Если ∆p начинает увеличиваться, итерационный процесс следует закончить. Тогда максимальная достигнутая точность оценивается относительной погрешностью
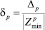(10)
для последнего р.
В векторной форме система (8) кратко выглядит так:
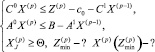
Средние значения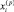 
и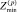 
можно также найти путём усреднения системы (8) с учётом (2) и (3):
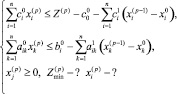
В частности, при р = 1
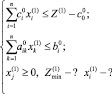
Эта система в точности совпадает с (5). Поэтому
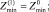
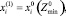
т.е. средние значения первого приближения совпадают с нулевым приближением.
При рассмотрении задачи на максимум Z следует во всех вышеприведённых неравенствах, содержащих Z, поменять знак неравенства с «≤» на «≥».
Пример
В работе [1] было найдено точное решение задачи:
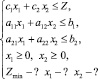
с коэффициентами:
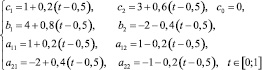(11)
Решение таково:
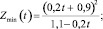
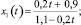x2 = 0. (12)
Усредняя (11) по формуле (2), находим
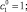
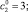
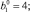
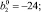
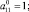
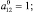
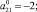
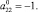(13)
|
|
||
|
|
|
|
|
|
|
|
|
|
||
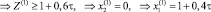
Решение в нулевом приближении [1]:
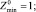
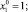
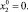(14)
Найдём решение в первом приближении. Для этого подставим в (6) значения (11), (13) и (14). Получаем систему неравенств:
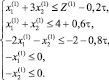
где обозначено τ = t – 0,5, τ ∈ [–0,5; 0,5].
Решаем её табличным способом [1]:
Таким образом,
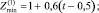
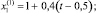
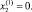(15)
Подставляя затем (11), (13), (15) в (7), находим решение во втором приближении:
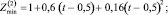
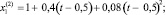
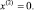(16)
Сравним значения Zmin, рассчитанные по (12), (15), (16):
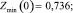
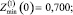
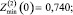
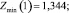
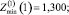
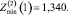
Их средние значения находим, усредняя (12), (15), (16) по формуле (2):
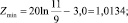
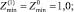
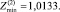
Оценим погрешности приближений (9), (10):
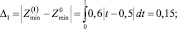
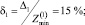
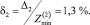
Отсюда видно, что если коэффициенты (11) при t ∈ [0;1] изменяются в пределах ±10 % по отношению к их средним значениям (13), то относительная погрешность конечного результата в первом приближении имеет тот же порядок малости. Во втором же приближении относительная погрешность результата порядка квадрата погрешности первого приближения, т.е. существенно меньше. Это согласуется с многочисленными другими задачами [4, 5].
Рецензенты:
Петров Л.Ф., д.т.н., профессор кафед_ры «Математические методы в экономике», ФГБОУ ВПО «РЭУ имени Г.В. Плеханова», г. Москва;
Титов В.А., д.э.н., профессор кафедры информационных технологий, ФГБОУ ВПО «РЭУ имени Г.В. Плеханова», г. Москва.