Целлюлозно-бумажная промышленность и лесопиление являются основными производствами, которые определяют эффективность использования леса и экономику лесопромышленного комплекса. Одной из важнейших операций этих производств является окорка. Эффективным использованием и высокими эксплуатационными показателями зарекомендовали себя цеповые окорочные установки фирм «Manitowoc», «Morbark», «Husky Brute» в зарубежной лесной промышленности. Особенно широко данный способ окорки распространен в США. Его используют при совмещении операций очистки от ветвей и сучьев и окорки ствола дерева. Цеповой орган позволяет обрабатывать спиленные и стрелеванные деревья и хлысты. Конечными продуктами являются окоренные круглые лесоматериалы с качеством окорки 90–98 % и потерями древесины до 3–8 %, топливная, зеленая щепа [1]. Для оценки внедрения данного способа окорки в отечественное использование необходимо изучить сущность процесса, его силовые и энергетические показатели.
Цель исследования – разработать математические модели процесса взаимодействия цепа и обрабатываемой поверхности лесоматериала для определения энергетических затрат и их зависимостей от режимных параметров технологического процесса.
Процесс цеповой окорки отличается от других известных способов. При цеповой окорке кора разрушается в результате воздействия на нее в нормальном направлении ударной силы. Определяющим в этом случае является уже предел прочности коры на сжатие поперек волокон.
Изучение процессов, происходящих при цеповой окорке древесины, производится путем рассмотрения возникающих при этом сил и их воздействия на обрабатываемый предмет [2]. Этот путь представляется не очень удачным. Эти силы действуют очень малое время, определить которое практически невозможно, следовательно, невозможно определить и величину этих динамических сил. Поэтому приходится ограничиваться общими теоретическими выкладками, а для получения практических рекомендаций проводить экспериментальные исследования. Мы предлагаем другой путь – исследовать не действующие силы, а затраты энергии, определить которые и аналитически, и практически значи тельно проще [5].
Одной из главных характеристик процесса цеповой окорки является интегральный показатель – удельная работа окорки k, которая является частным от деления работы окорки А на объем снятой коры G, то есть
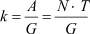 , (1)
, (1)
где N – мощность, затрачиваемая на окорку; T – время, в течение которого проходил процесс.
Размерность удельной работы окорки – Дж/м3 (в производстве обычно МДж/м3). На величину удельной работы процесса цеповой окорки оказывают основное влияние следующие факторы: масса звеньев цепов (m), число рядов цепов на приводном валу (цеповой головке, барабане) (Z), линейная скорость движения контактирующих цепов по обрабатываемой поверхности (VK), расстояние от крайнего звена до оси вращения (R), скорость подачи (надвигания) (U), площади поперечного сечения снимаемой ленты коры (F), количество звеньев, участвующих в контакте (nз).
Составим расчетную схему продольного взаимодействия цепа с поверхностью обрабатываемого объекта (рис. 1) [6]. Для упрощения представим цеп как набор точечных масс m, соединенных между собой с шагом t невесомыми нитями и вращающимися с угловой скоростью ω. Расстояние от центра звена до оси вращения – R1; расстояние от центра следующего звена до оси вращения – R2 и т.д.; R1 – R2 = t; h – расстояние от центра вала до обрабатываемой поверхности.
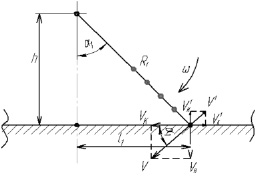
Рис. 1. Момент касания поверхности первым звеном: h – расстояние от центра вала до обрабатываемой поверхности; α1 – угол встречи конечного звена цепа и обрабатываемой поверхности; R1 – расстояние от центра конечного звена до оси вращения цепа; ω – угловая скорость вращения цепа; V – линейная скорость цепа в момент касания с поверхностью; V1 – скорость отскока цепа в результате контактного взаимодействия; l1 – расстояние от вертикали, проходящей через центр вала до точки контакта первого звена с поверхностью
Сначала рассмотрим случай, когда обрабатываемая поверхность неподвижна, т.е. движения подачи нет. Процесс протекает следующим образом. Цеп, вращаясь с угловой скоростью ω, подходит к обрабатываемой поверхности, и первое звено касается её с линейной скоростью V. Происходит косой удар под углом α1 к поверхности. Если бы масса первого звена m не находилась под действием центробежной силы и звено не было бы связано с остальными звеньями, то, согласно теории удара, произошел бы обыкновенный отскок (рикошет). Угол отскока не равен углу падения и определяется величиной коэффициента мгновенного трения, который зависит от состояния шероховатости поверхности и находится экспериментальным путем. При абсолютно гладкой поверхности угол отражения равен углу падения, а при шероховатой – меньше.
В нашем случае этого не произойдет, и отскок произойдет по закону маятника, т.е. в обратном направлении по дуге качания. При малых значениях угла α1 не исключен и первый вариант, но, в принципе, нас это не особенно интересует. Вопрос очень сложный и требует специального исследования. Главное, что в том и другом случае произойдет отскок массы после удара. Скорость его V1 будет равна произведению линейной скорости в момент касания с поверхностью V на коэффициент упругого восстановления kв [3, 4]. Нормальные (VH и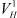 ) и касательные (VK и
) и касательные (VK и 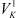 ) составляющие этих скоростей направлены в противоположные стороны.
) составляющие этих скоростей направлены в противоположные стороны.
Кинетическая энергия удара массы m со скоростью VH в нормальном направлении –
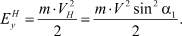 (2)
(2)
Энергия упругого восстановления –
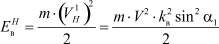 . (3)
. (3)
Соответственно кинетическая энергия разрушения поверхности первым звеном
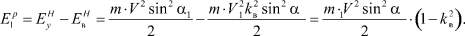 (4)
(4)
Эта энергия полностью пойдет на деформирование коры в нормальном направлении, т.е. на сжатие её поперек волокон.
Рассмотрим момент касания второго звена (рис. 2). Точка контакта первого звена с поверхностью (I) находится на расстоянии l1 = R1sinα1 от вертикали, проходящей через центр вала. Аналогично точка касания второго звена (II) будет находиться на расстоянии l2 = R2sinα2. Масса первого звена за этот промежуток времени переместится по поверхности объекта из точки (I) в точку (I1) на расстояние l1 – l2 – t (т.е. R1sinα1 – R2sinα2 – t)), совершая работу трения.
Кинетическая энергия разрушения вторым звеном будет
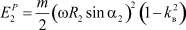
или
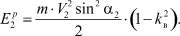 (5)
(5)
Эта величина меньше, чем 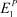 , так как R2 < R1 и α2 < α1. Таким образом, за один оборот вала цепа будет нанесен ряд ударов уменьшающейся силы от максимума в точке (I) до нуля в точке под осью вала.
, так как R2 < R1 и α2 < α1. Таким образом, за один оборот вала цепа будет нанесен ряд ударов уменьшающейся силы от максимума в точке (I) до нуля в точке под осью вала.
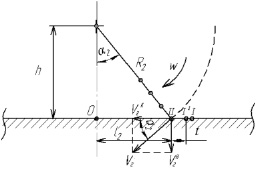
Рис. 2. Момент касания второго звена: α1 – угол встречи конечного звена цепа и обрабатываемой поверхности; R2 – расстояние от центра второго звена до оси вращения цепа; ω – угловая скорость вращения цепа; V – линейная скорость цепа в момент касания с поверхностью; V1 – скорость отскока цепа в результате контактного взаимодействия; l1 – расстояние от вертикали, проходящей через центр вала до точки контакта первого звена с поверхностью
Общая энергия разрушения в нормальном направлении –
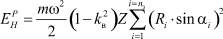
или
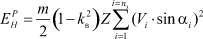 , (6)
, (6)
где nз – количество звеньев, участвующих в контакте (в целых числах) 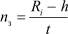 .
.
Расстояние между точками ударов также уменьшается. Если 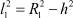 а
а 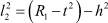 , то
, то 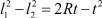 (выкладки опускаем).
(выкладки опускаем). 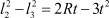 ;
; 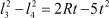 и так далее.
и так далее.
Касательная составляющая линейной скорости первого звена в первой точке взаимодействия 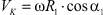 , а в точке О, находящейся под осью вращения
, а в точке О, находящейся под осью вращения 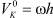 . Если учесть, что расстояние от центра вала до обрабатываемой поверхности
. Если учесть, что расстояние от центра вала до обрабатываемой поверхности 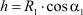 , то получится, что эти скорости равны. Отсюда следует вывод, что все звенья цепа, вступающие в контакт с обрабатываемой поверхностью, двигаются по ней с одинаковой скоростью VK, равной ωh [6].
, то получится, что эти скорости равны. Отсюда следует вывод, что все звенья цепа, вступающие в контакт с обрабатываемой поверхностью, двигаются по ней с одинаковой скоростью VK, равной ωh [6].
В отсутствии скорости надвигания при следующем обороте звенья цепа ударят по тем же самым местам. При наличии попутной U удар будет происходить с некоторым сдвигом, шагом удара е относительно предыдущих точек. Величину этого шага можно определить из основного кинематического соотношения 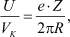 откуда
откуда 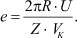
Разрушение коры от ударов звеньев цепа в нормальном направлении будет происходить только в первой половине общей зоны контакта от точки I до точки О (рис. 2).
Вернемся к рис. 1. Составляющая линейной скорости VK дает энергию разрушения в касательной плоскости первым звеном
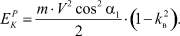
Если энергия в нормальном направлении полностью поглотится деформацией коры (вплоть до прессования), то энергия в касательном направлении будет востребована лишь частично. Она затратится на скалывание вдоль волокон, перемещение массы m по поверхности (контакт массы с поверхностью может и не потеряться за счет прижима центробежной силой, а если и потеряется, то через несколько мгновений после отскока восстановится, и цеп будет волочиться), истирание несколотых остатков коры и т.п. Все эти составляющие значительно меньше деформативной. Наиболее существенное из них – волочение цепа по поверхности обработки.
Сила трения при перемещении звена массой m равна mgμ, где mg – сила тяжести, μ – коэффициент трения металла звена по древесине или коре. Энергия на горизонтальное перемещение первого звена равна mgμ∙2l1, второго звена – mgμ∙2l2 и так далее. Общая энергия на перемещение цепа по обрабатываемой поверхности за один оборот вала
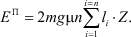 (7)
(7)
По абсолютной величине эта энергия значительно меньше, чем EP. Остаток энергии в касательном направлении тратится на движение цепа и на процесс непосредственной окорки не влияет.
Общая энергия, создаваемая первым звеном, определится как сумма (4) и (6)
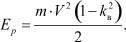 (8)
(8)
Рассматривая последовательно работу звеньев в касательной плоскости и суммируя её с энергией в нормальной плоскости, получим общую энергию разрушения, которую способен отдать цеп за один оборот
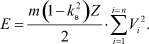
Эту зависимость можно выразить в ином виде:
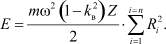
В зависимости от кинематических параметров процесса этого количества энергии может не хватить для качественной окорки, а может быть и излишним, когда производится чрезмерное измельчение коры. Всё зависит от конкретных условий: угловой скорости, скорости надвигания, массы рабочей части цепа, толщины коры, её физико-механических свойств и т.п. В идеальном случае создаваемая цепом энергия соответствует 100 % окорки. Решение в этом случае зависит от свойств коры не только на сдвиг или скалывание вдоль волокон (что более изучено), но и от смятия поперек волокон и удар – (что совершенно не изучено).
Когда за один проход цеп полностью производит окорку без лишних затрат энергии, удельная работа окорки k выразится как общая энергия разрушения цепом, отнесенная к объему снятой коры G.
За один оборот этот объем равен G = e∙F∙Z. Из рассмотренного следует, что удельная работа окорки
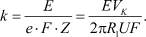
Непосредственно на окорку затрачивается работа (6) и (8), с учетом этого удельная работа окорки определится как
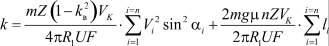
или
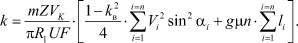 (9)
(9)
Выводы
Из данной математической модели следует вывод, что удельная работа окорки имеет кубическую зависимость от линейной скорости цепа, а от скорости подачи – обратную. Разработанные математические модели удельной работы процесса цеповой окорки позволяют определить энергетические затраты рабочих режимов с учетом влияния на элементы конструкции эксплуатационных и конструктивных факторов.
Рецензенты:
Полетайкин В.Ф., д.т.н., профессор, заведующий кафедрой технологии и машин природообустройства, ФГБОУ ВПО «Сибирский государственный технологический университет», г. Красноярск;
Козинов Г.Л., д.т.н., профессор, заведующий кафедрой промышленного транспорта и строительства, ФГБОУ ВПО «Сибирский государственный технологический университет», г. Красноярск.
Работа поступила в редакцию 21.05.2014.



