В настоящее время наблюдается большой интерес к проблеме распространения волн в газожидкостных системах (гидродинамические процессы современной технологии и энергетики, ультразвуковые технологии); реальная жидкость рассматривается двухфазной средой с начальными параметрами газосодержания, соответствующими экспериментальным данным. При описании движения газожидкостной смеси используются различные приближенные модели, в том числе уравнение Клейна ‒ Гордона [1, 4]. На основе этих моделей проводится изучение акустических свойств жидкостей с пузырьками газа, исследуются волны с конечной амплитудой в смесях с крупными пузырьками. Описываются взрывные неустойчивости поверхностей жидкого металла во внешнем электрическом поле и диэлектрической жидкости, а также тангенциальный разрыв по механизму Кельвина ‒ Гельмгольца и др. Уравнение синус-Гордона и его модификации применяются и при описании нелинейных сейсмических эффектов в геофизических средах наряду с известными математическими моделями (канонические нелинейные уравнения Бусинеска, Бургерса, Кортевега де Фриза, Шредингера). Здесь диссипация и дисперсия (основные характеристики геофизической среды и волновых процессов, протекающих в ее пределах) рассматриваются как существенные нелинейности.
Ниже исследуется решение одной конкретной модификации уравнения Клейна ‒ Гордона и обсуждаются возможности обобщений полученных результатов (частично рассматривались в [1…5]). Особое внимание уделяется решению типа бегущей волны, сглаживающейся на бесконечности (решение вида φ(x, t) = g(x – v·t), отличное от константы, у которого g(ξ) стремятся к константам при ξ → +∞ и при ξ → –∞, и у которого g′(ξ) стремятся к нулю при ξ → +∞ и при ξ → –∞).
Предварительно рассмотрим уравнение Клейна ‒ Гордона:
φxx(x, t) – φtt(x, t) = f(φ(x, t)). (1)
Сделаем замену φ(x, t) = g(ξ), где ξ = x – v·t. При v ≠ ±1 уравнение (1) эквивалентно
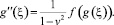
Умножая на g′(ξ), после интегрирования получим:
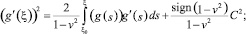
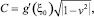
где ξ0 – произвольная точка того промежутка, где определена g(ξ).
По определению классического решения дифференциального уравнения второго порядка функция g(ξ) должна иметь второй порядок гладкости. Если f(ζ) непрерывна на ¡, то к интегралу в правой части можно применить теорему о замене переменной в определенном интеграле:
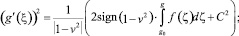g0 = g(ξ0). (2)
Пусть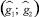 
– промежуток строгой монотонности функции g(ξ) и пусть 
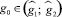; правая часть (2) – положительна и можно к (2) применить теорему об обратной функции:
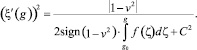
Таким образом, чтобы решение φ(x, t) было бегущей волной, сглаживающейся на бесконечности, необходимо и достаточно расходимости интеграла
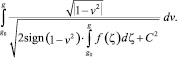
при
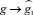и при 
.
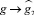Воспользуемся приведенным методом для исследования одной модификации уравнения синус-Гордона (частный случай уравнения Клейна ‒ Гордона):
φxx(x, t) – φtt(x, t) = sin(φ(x, t)) + sin(2l·φ(x, t)), l ≥ 2. (3)
Будем искать решение в виде φ(x, t) = g(ξ), где ξ = x – v·t. Тогда:
(1 – v2)·g″(ξ) = sin(g(ξ)) + sin(2l·g(ξ)), l ≥ 2. (4)
В случае v = ±1 получим, что 0 = in(g(ξ)) + sin(2l·g(ξ)) или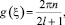 
n ∈ ¢ и 
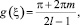m ∈ ¢. Решение – константа, что противоречит определению бегущей волны, сглаживающейся на бесконечности.
При v ≠ ±1 уравнение (4) эквивалентно системе:
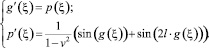(5)
Теорема. При v ≠ ±1 у уравнения (3) существуют решения типа бегущей волны, сглаживающейся на бесконечности.
При v ≠ ±1 решения уравнения (3) будут типа бегущей волны, сглаживающейся на бесконечности, если g′(ξ) будет стремиться к нулю и при ξ → +∞, и при ξ → –∞.
Для доказательства изучим положения равновесия системы (4). Поскольку правые части этой системы периодически зависят от g, то ее особые точки делятся на несколько видов в зависимости от значения g:
1. 
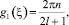n ∈ ¢.
2. 
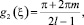m ∈ ¢.
В первом случае имеем:
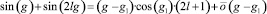
(cos(g1) = 0 только пр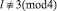и
и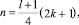 
k ∈ ¢; здесь и далее предполагается, что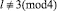 
).
Систему (5) можно переписать в виде
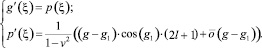
Собственные значения λ определятся из уравнения:
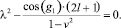(6)
Отсюда видно, что в зависимости от λ особая точка может быть разных типов:
– седло при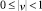 
(уравнение (6) имеет два корня разных знаков);
– центр при |v| > 1.
Из теоремы о положении равновесия по первому приближению известно, что если собственные значения чисто мнимые, то первое приближение может не давать ответа на вопрос о типе особой точки. В рассматриваемом случае будут центры (замкнутые траектории, гомотопные окружностям, охватывают особую точку).
Исследуем исходную нелинейную систему (5). Умножив первое уравнение системы на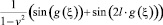 
, а второе – на p(ξ), на фазовой плоскости получим семейство линий:
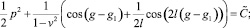
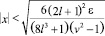или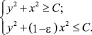 
Расстояние между границами этих областей (внешность окружности и внутренность эллипса)
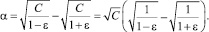
При ε ≤ 0,5 справедливо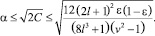 
Справедливы утверждения (лемма): если выполнены условия:
1. 
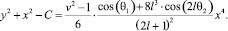
2. 
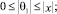
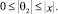
3. 
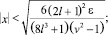
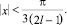
4. 
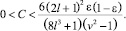
5. 
,
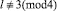то множество точек (x, y) заключено между окружностью (внутренняя граница)
y2 + x2 – C ≥ 0
и эллипсом (внешняя граница)
y2 + (1 – ε)·x2 – C ≤ 0.
Рассмотрим особые точки, в окрестности которых:
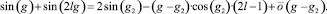
Здесь точки распадаются на два подсемейства:
a)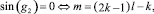 
k ∈ ¢ ⇔
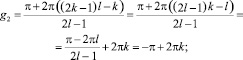
b)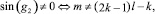 
k ∈ ¢.
В случае а) систему (5) можно представить в виде
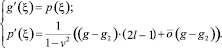
Собственные значения λ определяются из уравнения:
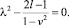(7)
При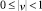 
(уравнение (7) имеет два корня разных знаков) особая точка есть седло; центр – при |v| > 1 (уравнение (7) имеет два чисто мнимых корня).
В случае b) систему (5) можно представить в виде:
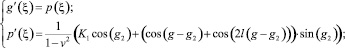
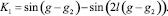
Фазовые портреты системы (5) представлены на рис. 1, 2.
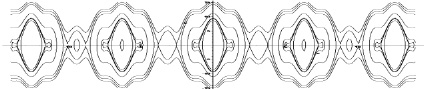
Рис. 1. Фазовый портрет системы (5) при |v| > 1
Рис. 2. Фазовый портрет системы (5) при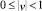 
Лемма. Если фазовая траектория пересекает ось абсцисс не в особой точке, то она проходит цикл полностью на конечном промежутке изменения параметра.
Действительно, умножив уравнение (4) на g′, проинтегрировав полученное равенство и перейдя к обратной функции ξ = ξ(g), получим:
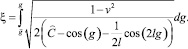(8)
Для доказательства леммы необходимо показать, что в точках g0, где знаменатель обращается в нуль, интеграл сходится. Следует отметить, что это именно те точки, где фазовые линии пересекают ось абсцисс. Разложим знаменатель в ряд Тейлора с остаточным членом в форме Пеано в окрестности точки g0:
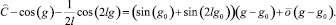
Заметим, что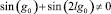 
, так как g0 не является особой точкой. По признаку сравнения интеграл (8) будет сходиться – значение ξ конечно. Лемма доказана.
Замечание. В случае, когда g0 – особая точка, интеграл (8) будет расходиться – значение ξ бесконечно.
Имеем:
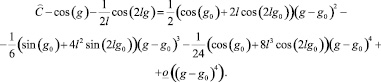
По признаку сравнения интеграл расходится (непосредственной подстановкой можно убедиться, что коэффициент либо при 2 степени, либо при 3 степени отличен от нуля).
Можно показать, что фазовые траектории системы (5) имеют вид, приводимый на рис. 3, 4. Умножив первое уравнение системы на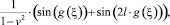 
а второе – на p(ξ), получим на фазовой плоскости семейство линий:
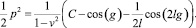
При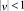 
(множество особых значений постоянной C – это
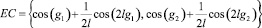
возможны случаи (рис. 3):
1. 
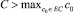, тогда p2 > 0, а значит, g′(ξ) ≠ 0 при любом ξ.
2. C ∈ EC, тогда p2 ≥ 0 при любом ξ. Причем p2 = 0 тогда и только тогда, когда рассматриваемая траектория пересекает ось абсцисс в особых точках первого вида.
3. 
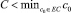, тогда p2 < 0, а значит, решений не существует.
4. Иначе траектории пересекают ось абсцисс в точке, которая не совпадает с особыми точками, а значит, к этому случаю применима лемма.
Итак, решение типа волны, сглаживающейся на бесконечности, существует.
При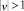 
(множество особых значений постоянной С – это
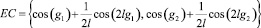
возможны случаи (рис. 4):
1. 
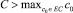, тогда p2 > 0, а значит, g′(ξ) ≠ 0 при любом ξ.
2. C ∈ EC, тогда p2 ≥ 0 при любом ξ. Причем p2 = 0 тогда и только тогда, когда рассматриваемая траектория пересекает ось абсцисс в особых точках первого вида.
3. 
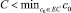, тогда p2 < 0, а значит, решений не существует.
4. Иначе траектории пересекают ось абсцисс в точке, которая не совпадает с особыми точками, а значит, к этому случаю применима лемма.
Итак, решение типа волны, сглаживающейся на бесконечности, существует.
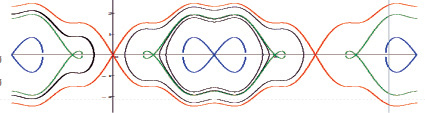
Рис. 3. Фазовый портрет системы(5) при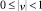 
(траектории уединенных волн отмечены красным, зеленым и синим)
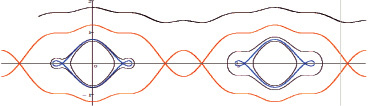
Рис. 4. Фазовый портрет системы (5) при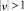 
(траектории уединенных волн отмечены красным и синим)
Теорема доказана.
Заключение
Доказано, что уравнение (3) в случае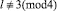 
имеет решения типа уединенной волны; приведены формулы для этих решений. Результаты исследований легко обобщить на случай уравнения Клейна ‒ Гордона с произвольной правой частью; могут быть использованы при изучении эффекта Джозефсона и решения других задач, приводящих к уравнению Клейна ‒ Гордона и их модификациям (для исследования нелинейных сейсмических эффектов и процессов, в технологиях связи, в волновой генетике).
Рецензенты:
Голованов О.А., д.ф.-м.н., профессор кафедры общепрофессиональных дисциплин Пензенского артиллерийского инженерного института, г. Пенза;
Камбург В.Г., д.т.н., профессор кафедры информационно-вычислительных систем Пензенского государственного университета архитектуры и строительства, г. Пенза.
Работа поступила в редакцию 26.03.2014.