Если задан ряд положительных целых чисел p1, p2, …, pn, называемых основаниями (модулями) системы, то под системой счисления в остаточных классах (СОК) понимают такую систему, в которой целое число X ∈ [0, P – 1], где P = p1∙p2∙...∙pn, представляется в виде остатков по выбранным основаниям [1, 7]:
(1)
т.е. цифра i-го разряда xi числа 
, называемого модулярным числом, есть наименьший неотрицательный остаток от деления позиционного числа X на pi. Если все pi попарно взаимно простые, то между множеством {X│X ∈ [0, P – 1]} и множеством кортежей 
однозначным образом определяется биекция 
, причем прямое преобразование задается в соответствии с (1), а обратное определяется формулой
(2)
Здесь числа Bi представляют собой ортогональные базисы СОК [1].
Определенная таким образом система обладает рядом важных достоинств. Отдельные разряды модулярных чисел малоразрядные и могут обрабатываться без учета переносов между ними, поэтому СОК отвечает многоядерной архитектуре современных вычислительных устройств. На основе СОК могут быть построены эффективные параллельные алгоритмы для решения задач из самых разнообразных областей знаний. Базовые арифметические операции в СОК делятся на следующие две группы [1, 7].
1. Модульные операции, которые могут быть выполнены параллельно и независимо над отдельными цифрами чисел (1), например, сложение, умножение, вычитание без знака и т.д.
2. Немодульные операции, которые требуют знания величины модулярных чисел в целом. К данной группе относятся: сравнение, вычитание с получением отрицательного результата, контроль переполнения модулярного числа и т.д.
Основным фактором, сдерживающим широкое применение СОК на практике, является неочевидность выполнения немодульных операций [1, 3, 5–7].
1. Выполнение немодульных операций в системе остаточных классов
Для выполнения немодульных операций в СОК применяются, как правило, точные методы, основанные на вычислении точных позиционных характеристик модулярных чисел. Всякая позиционная характеристика представляет собой выраженную тем или иным способом информацию о позиционном значении модулярного числа (1). К наиболее известным точным позиционным характеристикам относятся коэффициенты обобщенной позиционной системы счисления (ОПСС), ранг, след, функция ядра и т.д. [1, 3, 7]. Недостатком методов, основанных на вычислении точных позиционных характеристик, является их высокая временная либо аппаратная сложность реализации [7].
Альтернативой точных является приближенный метод выполнения немодульных операций [5, 6]. Он основан на вычислении приближенной позиционной характеристики, которая представляет собой округленное до машинного представления значение отношения анализируемого модулярного числа к произведению модулей СОК. Вычисление приближенной характеристики осуществляется за малое время и при этом не требует хранения больших подстановочных таблиц. При знании приближенных характеристик чисел в СОК операции определения знака, сравнения, обнаружения ошибки и переполнения выполняются простым образом [5, 6]. Однако погрешности округления, возникающие в ходе вычисления приближенной характеристики, могут приводить к некорректному выполнению немодульных операций. Оценить эти погрешности и определить, что операция выполнена некорректно, весьма сложно без знания позиционного значения соответствующего модулярного числа. Это затрудняет использование приближенного метода на практике.
2. Метод выполнения немодульных операций на основе интервальных позиционных характеристик
Определение. Всякую немодульную операцию над модулярными числами будем называть достоверной тогда и только тогда, когда ее результат либо является корректным, либо за время, сопоставимое со временем выполнения данной операции, может быть доказательно определена невозможность получения корректного результата.
Решить проблему достоверности приближенного метода выполнения немодульных операций, сохранив при этом его преимущества, заключающиеся в низкой вычислительной и аппаратурной сложности, позволяет метод, основанный на применении интервальных позиционных характеристик. Предлагаемый метод опирается на базовые концепции интервальных (достоверных, доказательных) вычислений [2, 4] и состоит в следующем.
Пусть в СОК с модулями P = p1, p2, ..., pn задано модулярное число 
. Пусть 
– точное значение отношения 
, где P = p1∙p2∙...∙pn. 
по определению представляет собой рациональное число, разрядность которого определяется разрядностью P и может быть в общем случае много больше разрядности вычислительного устройства.
Определение. Вещественный интервал 
с рациональными границами 
и 
, направленно округленными до размера разрядной сетки вычислительного устройства и отвечающими условию 
, называется интервальной позиционной характеристикой модулярного числа 
. Стоит различать интервальную позиционную характеристику и интервальный номер модулярного числа [1].
Границы, задающие интервальную позиционную характеристику, определяются с помощью направленных округлений: нижняя граница округляется до ближайшего машинного числа с недостатком, а верхняя – с избытком:
(3)
где 
Здесь операторы ↓ и ↑ отвечают округлениям с недостатком и избытком соответственно. Техника выполнения этих округлений для различных способов представления чисел неоднократно освещалась в литературе (см., например, работы [3, 8]).
Интервальная позиционная характеристика 
модулярного числа 
позволяет единообразным способом учесть погрешности округлений, неизбежно возникающие при сопоставлении точному значению 
представления с ограниченной разрядностью: 
заключается в гарантированно содержащие это значение границы, направленно округленные до разрядности машинного представления. При этом погрешности округлений лишь несколько расширяют границы, оставляя включение 
истинным.
Пример. Пусть p1 = 7, p2 = 9, p3 = 11, p4 = 13 – модули СОК, P = 9009 – их произведение,
– соответствующие мультипликативные инверсии [1, 7]. Тогда интервальная позиционная характеристика модулярного числа 
определится в соответствии с (3) следующим образом:
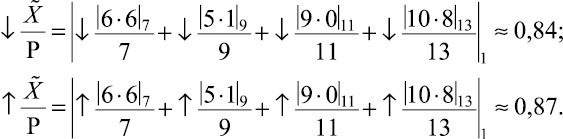
Таким образом, 
, причем гарантируется, что точное значение 
лежит в указанном интервале. В соответствии с (2), 
, поэтому 
.
Определение. Для любого модулярного числа 
его интервальная позиционная характеристика 
является корректной тогда и только тогда, когда 
.
Необходимым условием правильного выполнения немодульных операций над модулярными числами 
и 
с помощью их интервальных позиционных характеристик 
и 
соответственно является корректность как 
, так и 
.
Определение. Диаметром интервальной позиционной характеристики называется разность ее верхней и нижней границ:
(4)
Погрешности округления границ при вычислении интервальной позиционной характеристики прямым образом отражаются в ее диаметре [4]. Если для машинного представления границ отведено k двоичных разрядов, а модулярное число задается n k-разрядными модулями СОК, то 
Определение. Пусть 
и 
– интервальные позиционные характеристики модулярных чисел 
и 
соответственно. Тогда отношение
суть теоретико-множественное пересечение 
и 
.
Если пересечение не пусто, то его результат может быть представлен интервалом
причем в этом случае в соответствии с (4) 
. Если 
то 
. Если 
и 
пересекаются, то справедливо одно из утверждений:
1. Модулярные числа 
и 
равны. В этом случае всякая немодульная операция над ними выполняется интуитивным образом.
2. Модулярные числа различны, но отношение их разности к произведению модулей СОК находится в пределах погрешностей, определяющих диаметры характеристик 
и 
. В этом случае выполнение всякой немодульной операции над числами 
и 
при помощи 
и 
может дать некорректный результат, поэтому следует прибегнуть к использованию точных методов, например, преобразовав 
и 
в ОПСС.
Таким образом, достаточным условием корректности выполнения немодульных операций над модулярными числами 
и 
с помощью их интервальных позиционных характеристик 
и 
является пустое пересечение 
.
Теорема. Если для модулярных чисел 
и 
их интервальные характеристики 
и 
корректны (см. определение выше), а 
, то результат всякой немодульной операции над 
и 
, выполняемой при помощи 
и 
, будет корректным.
Доказательство теоремы исходит из замечания, что большинство немодульных операций над модулярными числами, так или иначе, сводятся к сравнению по величине этих чисел. Поэтому можно считать, что немодульная операция над 
и 
, выполняемая при помощи 
и 
, некорректна, если истинно одно из следующих утверждений:
Далее доказывается невозможность выполнения ни одного из этих утверждений.
Представленная теорема является обоснованием достоверности немодульных операций. Это означает, что всякая немодульная операция над модулярными числами, выполняемая с помощью их интервальных позиционных характеристик, либо будет выполнена корректно, либо будет сделан вывод о невозможности ее корректного выполнения. Арифметические операции сложения и вычитания интервальных характеристик определяются следующими формулами [2, 4]:
(5)
(6)
Умножение и деление определяется аналогичным образом [6, 7]. Правила выполнения основных немодульных операций в СОК с использованием интервальных позиционных характеристик модулярных чисел аналогичны правилам, справедливым для точечного представления приближенной позиционной характеристики, представленным в работах [5, 6]. Пусть, например, 
и 
– модулярные числа, а 
и 
– их интервальные позиционные характеристики, вычисленные в соответствии с (3) и отвечающие необходимому и достаточному условиям корректности немодульных операций. Тогда сравнение по величине 
и 
определится следующим образом:
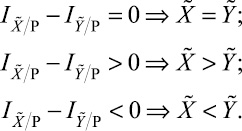
Определение переполнения при сложении чисел в СОК выполняется следующим образом:
Аналогично определяются и другие немодульные операции, такие как контроль переполнения при умножении, определение знака модулярного числа в дополнительном коде, вычитание с возможностью получения отрицательного результата и т.д.
Примеры. Будем использовать следующие модули СОК: p1 = 7, p2 = 9, p3 = 11, p4 = 13, их мультипликативные инверсии:
1) Выполним сравнение 
и 
. Для этого определим их интервальные характеристики в соответствии с выражением (3), округляя границы до двух разрядов:
таким образом 
, 
. Данные характеристики корректны, а 
поэтому заключаем, что операция сравнения чисел 
и 
с их помощью будет выполнена верно. Выполняя вычитание в соответствии с (6), получим
,
поэтому 
. И действительно
2) Пусть 
, 
и требуется определить, произойдет или нет переполнение при их сложении. Определяем интервальные позиционные характеристики: 
, 
. Данные характеристики отвечают необходимому и достаточному условиям корректности выполнения немодульной операции. В соответствии с (5) имеем:
,
следовательно, при сложении 
и 
произойдет переполнение. В правильности полученного вывода можно убедиться, преобразовав операнды в позиционную систему:
Вычисление первой границы интервальной характеристики требует n обращений к LUT-памяти за значениями мультипликативных инверсий, n умножений, n делений и одну операцию n-операндного суммирования с отбрасыванием целой части, которая выполнится (последовательно) также за n тактов. При вычислении второй границы значения произведений модулярных разрядов и соответствующих мультипликативных инверсий (слагаемые Ni в (3)) уже будут вычислены, поэтому необходимо лишь поделить их на модули СОК, округлив соответствующим образом, и сложить. Таким образом, вычисление интервальной позиционной характеристики требует выполнения 6n операций над машинными числами (n – количество модулей СОК). Для сравнения, алгоритм Гарнера [3], основанный на использовании в качестве позиционной характеристики коэффициентов ОПСС, требует для их определения в среднем n2 операций.
Заключение
Предложен асимптотически быстрый метод выполнения немодульных операций в СОК, основанный на использовании интервальных позиционных характеристик для оценки величины модулярных чисел. Данный метод обеспечивает достоверность выполняемых операций в отличие от приближенного метода и не требует больших вычислительных либо аппаратурных затрат в отличие от известных точных методов. Алгоритм вычисления интервальных позиционных характеристик не требует работы с числами, выходящими за пределы разрядной сетки, а его временная сложность линейна по количеству модулей СОК. Таким образом, предложенный метод является полезной альтернативой известным методам выполнения немодульных операций в СОК.
Рецензенты:
Частиков А.В., д.т.н., профессор, декан факультета прикладной математики и телекоммуникаций Вятского государственного университета, г. Киров;
Страбыкин Д.А., д.т.н., профессор, заведующий кафедрой электронных вычислительных машин Вятского государственного университета, г. Киров.
Работа поступила в редакцию 22.02.2013