Tacho-Godi А.Z. 1
1 Donskoy state agrarian university
The work gives the information about the simulation of the wave of voltages at explosive impact in the subject of the coal mining enterprises with the help of the numerical method Musayev V.K. in displacements. The explosive effects are modeled in the form of a Delta function. The target area has 17112 the nodal points. Solved by a system of equations of 68448 unknown. Shows the normal stresses in the characteristic points of the investigated area in an explosive impact. Problems can be solved with the help of numerical simulation of two-dimensional plane wave equation of the theory of elasticity. The problem is solved by the method of end-to-end accounts, without identifying gaps. The main equations of a method of finite elements in displacements is obtained with the help of the principle of virtual displacements. For approximation of the study area apply triangular and rectangular finite elements of the first order. We obtain an explicit two-layer finite-element scheme.
modeling
wave
a characteristic area
an explosive effect
object
coal mining enterprise
a numerical method
move
normal voltage
elasticity theory
finite elements
algorithm
a set of programs
the method of end-to-end accounts
1. Musayev V.K. Solution to the problem of diffraction and propagation of elastic waves by finite element method // Structural Mechanics and analysis of structures. 1991. no. 4. pp. 74–78.
2. Musayev V.K. Numerical solution of the wave of elasticity and plasticity // Bulletin of the Russian University of Peoples’ Friendship. Series Applied Mathematics and Computer Science Applied Mathematics and Computer Science. 1997. no. 1. pp. 87–110.
3. Musayev V.K. .Numerical modeling of the stress of building structures with time-dependent dynamical effects // Architecture shells and strength raset walled construction and engineering design of complex shape. Works of the International Conference. – V.: the Russian University of Peoples’ Friendship. 2001. pp. 289–296.
4. Musayev V.K. Numerical solution of some problems of life safety with the finite element method // Bulletin of the Russian University of Peoples’ Friendship. A series of complex security problems. 2005. no. 1. pp. 17–23.
5. Musayev V.K. Destruction, complex deformable bodies caused by impulses // Bulletin of the Russian University of Peoples’ Friendship. A series of complex security problems. 2006. no. 1. pp. 36–42.
6. Musayev V.K. Some possibilities of mathematical modeling and numerical computer simulation // Bulletin of the Russian University of Peoples’ Friendship. A series of complex security problems. 2006. no. 1. pp. 81–86.
7. Taho-Gody A.Z., Sitnik S.V., Kurantsov V.V., Kormilitsin A.I., Akatiev S.V. Reliability of the results of the numerical method Musayev V.K. the displacement for the problem of the reflection of elastic stress waves in the form of a delta function from the free surface // Technosphere safety, reliability, quality, energy and resource conservation: Vol. 38. Materials of International scientific and practical conference. Edition VIII. Vol. 2. Rostov-on-Don: Rostov State University of Civil Engineering. 2011. pp. 280–284.
8. Taho-Gody A.Z. A method for the unsteady wave problems using numerical method Musayev V.K. in displacement // Materials of International scientific and practical conference «Safety and ecology of technological processes and productions». Village Persianovskiy of Rostovregion: Don State Agrarian University. 2012. pp. 73–78.
9. Taho-Gody A.Z. Modeling of wave voltage at explosive impact of coal mines in the objects using a numerical method Musayev V.K. in displacement // Materials of International scientific and practical conference «Safety and ecology of technological processes and productions». Village Persianovskiy of Rostovregion: Don State Agrarian University. 2012. pp. 78–85.
10. Musayev V.K. Testing of stressed state in the structure-based system under non-stationary dynamic effects // Proceeding of the second International conference on recent advances in geotechnical earthquake engineering and soil dynamics. – Sent Louis: University of Missouri-Rolla. 1991. Vol. 3. pp. 87–97.
Поставленная задача реализуется с помощью уравнений математической нестационарной динамической теории упругости.
Некоторые результаты рассматриваемого численного метода приведены в следующих работах [1–7].
Рассмотрим задачу о воздействии сосредоточенного взрывного воздействия (рис. 2) в объекте неглубокого заложения на окружающую среду (рис. 1).
В точке C приложено нормальное сосредоточенное воздействие σy, которое при 0 ≤ n ≤ 10 (n = t/Δt) изменяется линейно от 0 до P, а при 10 ≤ n ≤ 20 от P до 0 (P = σ0, σ0 = –0,1 МПа – 0,1 МПа (–1 кгс /см2)).
Граничные условия для контура AIHG при t > 0 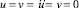 . Отраженные волны от контура AIHG не доходят до исследуемых точек при 0 ≤ n ≤ 150. Контур ABCDEFG свободен от нагрузок, кроме точки C, где приложено сосредоточенное взрывное воздействие.
. Отраженные волны от контура AIHG не доходят до исследуемых точек при 0 ≤ n ≤ 150. Контур ABCDEFG свободен от нагрузок, кроме точки C, где приложено сосредоточенное взрывное воздействие.
Расчеты проведены при следующих исходных данных:
H = Δx = Δy; Δt = 1,393∙10–6 с;
E = 3,15∙104 МПа (3,15∙105 кгс/см2);
ν = 0,2; ρ = 0,255∙104 кг/м3 (0,255∙10–5 кгс с2/см4);
Cp = 3587 м/с; Cs = 2269 м/с.
Исследуемая расчетная область имеет 17112 узловых точек. Решается система уравнений из 68448 неизвестных.
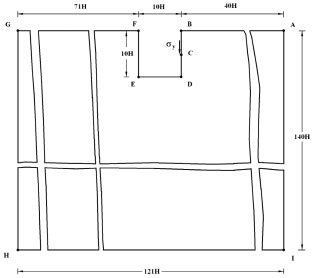
Рис. 1. Постановка задачи о сосредоточенном взрывном воздействии в объекте неглубокого заложения на окружающую среду
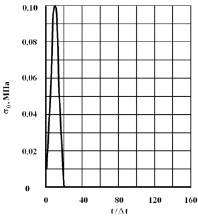
Рис. 2. Воздействие типа дельта функции
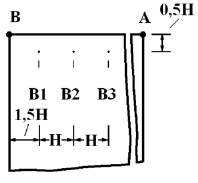
Рис. 3. Точки B1–B3, в которых приводятся упругие напряжения во времени
На рис. 4–6 показано изменение упругого нормального напряжения 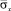 (
(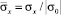 ) во времени n в точках B1–B3 (см. рис. 3), находящихся около свободной поверхности упругой полуплоскости.
) во времени n в точках B1–B3 (см. рис. 3), находящихся около свободной поверхности упругой полуплоскости.
Растягивающее упругое нормальное напряжение 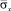 от точки B1 до точки В3 изменяется от значения
от точки B1 до точки В3 изменяется от значения 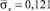 до значения
до значения 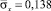 .
.
Сжимающее упругое напряжение 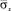 от точки B1 до точки В3 изменяется от значения
от точки B1 до точки В3 изменяется от значения 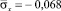 до значения
до значения  .
.
На основании проведенных исследований можно сделать следующие выводы:
1. Решена задача о сосредоточенном взрывном воздействии в объекте неглубокого заложения на окружающую среду. Взрывное воздействие моделируется в виде дельта функции. Исследуемая расчетная область имеет 17112 узловых точек. Решается система уравнений из 68448 неизвестных. Получены напряжения в характерных точках на поверхности упругой полуплоскости около объекта неглубокого заложения. Растягивающее упругое нормальное напряжение 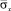 имеет следующее максимальное значение:
имеет следующее максимальное значение: 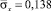 . Сжимающее упругое нормальное напряжение
. Сжимающее упругое нормальное напряжение 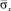 имеет следующее максимальное значение:
имеет следующее максимальное значение:  .
.
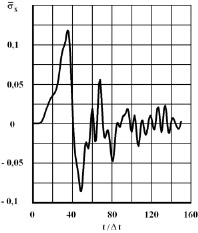
Рис. 4. Изменение упругого нормального напряжения во времени t/Δt в точке B1
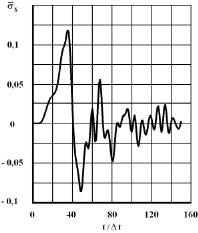
Рис. 5. Изменение упругого нормального напряжения во времени t/Δt в точке B2B2
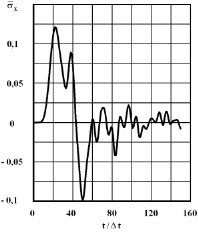
Рис. 6. Изменение упругого нормального напряжения во времени t/Δt в точке B3B3
2. Полученные результаты можно оценить как первое приближение о решении сложной комплексной задачи с помощью численного метода Мусаева В.К. для оценки напряженного состояния объектов угледобывающих предприятий при взрывных воздействиях.
Автор выражают благодарность Мусаеву В.К. за внимание к работе.
Рецензенты:
Мусаев В.К. Оглы, д.т.н., профессор, директор научно-производственной фирмы «Интерсейм», г. Пушкино;
Шаршак В.К., д.т.н., профессор кафедры «Механика, машины и оборудование пищевых производств» Донского государственного аграрного университета, г. Новочеркасск.
Работа поступила в редакцию 18.10.2012.
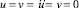 . Отраженные волны от контура AIHG не доходят до исследуемых точек при 0 ≤ n ≤ 150. Контур ABCDEFG свободен от нагрузок, кроме точки C, где приложено сосредоточенное взрывное воздействие.
. Отраженные волны от контура AIHG не доходят до исследуемых точек при 0 ≤ n ≤ 150. Контур ABCDEFG свободен от нагрузок, кроме точки C, где приложено сосредоточенное взрывное воздействие.



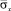 (
(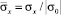 ) во времени n в точках B1–B3 (см. рис. 3), находящихся около свободной поверхности упругой полуплоскости.
) во времени n в точках B1–B3 (см. рис. 3), находящихся около свободной поверхности упругой полуплоскости.
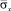 от точки B1 до точки В3 изменяется от значения
от точки B1 до точки В3 изменяется от значения 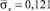 до значения
до значения 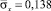 .
.
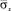 от точки B1 до точки В3 изменяется от значения
от точки B1 до точки В3 изменяется от значения 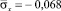 до значения
до значения  .
.
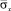 имеет следующее максимальное значение:
имеет следующее максимальное значение: 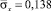 . Сжимающее упругое нормальное напряжение
. Сжимающее упругое нормальное напряжение 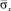 имеет следующее максимальное значение:
имеет следующее максимальное значение:  .
.






