Современный этап развития спецпроцессоров (СП) цифровой обработки сигналов (ЦОС) характеризуется разработкой и применением параллельных вычислительных устройств. В работах [1-3] показана целесообразность реализации ортогональных преобразований сигналов с использованием математических моделей, обладающих свойством кольца и поля, в частности, полиномиальной системы классов вычетов (ПСКВ). В данной системе в качестве модулей непозиционной системы используются неприводимые минимальные многочлены поля Галуа 
, что позволяет задать следующее отображение
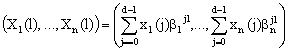, (1)
где 
.
Приравнивая соответствующие координаты, получаем n пар преобразования аналогичного ДПФ
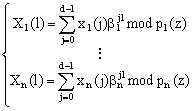, (2)
Применение ПСКВ позволяет свести вычисление ортогональных преобразований сигналов в поле Галуа над кольцом M(z) к n независимым вычислениям, проводимым по модулям pi(z). При этом вычисления организуются параллельно, помодульно и независимо друг от друга.
Характерной чертой всех арифметических устройств, функционирующих в ПСКВ, является необходимость выполнения суммирования по модулю 2. Следовательно от реализации данной операции во многом будет зависеть эффективность работы всего СП ЦОС. Качественным скачком в обеспечении реального масштаба времени является использование нейросетевого логического базиса (НЛБ). Структура алгоритма обработки данных, представленных в модульной ПСКВ, как и структура НЛБ обладает естественным параллелизмом, что позволяет эффективно использовать нейронные сети (НС) при реализации СП ЦОС [2,3].
Проведенный анализ известных алгоритмов реализации многовоховых сумматоров по модулю2 показал, что они обладают рядом недостатков, основным из которых является невозможность обучения нейронной сети. Для решения данной проблемы предлагается изменить треугольную функцию активации на активационную функцию:
. (3)
Данная функция может быть также определена с помощью предельного перехода
. (4)
Предлагается для обучения НС использовать генетические алгоритмы, которые обладают следующими преимуществами [5,6]:
- малочувствительность к нерегулярностям поведения целевой функции;
- высокая эффективность в поиске глобальных минимумов адаптивных рельефов;
- достаточно высокая скорость обучения;
- возможность оперировать дискретными значениями параметров НС, что упрощает аппаратную реализацию нейтронных сетей.
При обучении нейросетевого сумматора использовался мажоритарный генетический алгоритм с выделенной доминантой [6], что позволило оценивать степень приспособленности особи не только положительными значениями.
Для вычисления значения функции приспособленности формировались 2n, где n - число входов нейросетевого сумматора, двоичных векторов 
соответствующих различным стоянием входов сети. Далее для каждого двоичного вектора 
определялось значение на выходе нейронной сети 
и сумма по модулю 2 элементов двоичного вектора.
Модуль разности 
определяет ошибку в вычислении суммы по модулю 2 для двоичного вектора . Тогда как отрицательное значение суммы модулей разности для всех двоичных векторов использовалось для определения функции приспособленности особей популяции генетического алгоритма, иными словами
где μ - степень приспособленности особи в популяции; W1, W2- матрицы весовых коэффициентов нейтронов скрытого и выходного слоев соответственно; B1, B2 - вектор-столбец смещений нейронов скрытого и выходного слоя НС. Очевидно, что глобальным максимумом функции приспособленности является значение μ=0, когда для всех двоичных векторов выполняется равенство 
.
При обучении нейросетевого сумматора по модулю 2 удалось изменить его архитектуру таким образом, что весовые коэффициенты и смещения нейронов стали принадлежать трехэлементному множеству {-1;0;1}. На рисунке 1 представлена структура обученного четырехвходного сумматора по модулю 2.
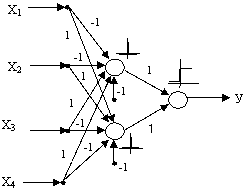
Рис. 1. Сумматор по модулю 2
В результате обучения получены следующие параметры нейронной сети
.
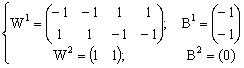Таким образом, очевидно, что применение генетических алгоритмов позволило улучшить структуру нейросетевого сумматора по модулю 2 за счет уменьшения динамического диапазона значений параметров НС. Кроме того, за счет анализа аргументов функции активации удалось упростить активационную функцию нейронов скрытого слоя НС.
СПИСОК ЛИТЕРАТУРЫ:
- Вариченко Л.В. Абстрактные алгебраические системы и цифровая обработка сигналов. - Киев: Наука думка, 1986. -.247 с.
- Элементы компьютерной математики и нейроноинфроматики /Червяков Н.И., Калмыков И.А. и др.; Под ред. Н.И. Червякова. - М.: Физматлит, 2003. - 216 с.
- Калмыков И.А. Математические модели нейросетевых отказоустойчивых вычислительных средств, функционирующих в полиномиальной системе классов вычетов/Под ред. Н.И. Червякова - М: Физматлит, 2005.-276 с.
- Калмыков И.А., Резеньков Д.Н., Тимошенко Л.И. Непозиционное кодирование для отказоустойчивых СП ЦОС //Инфокоммуникационные технологии, 2007, № 3 - С.36-38.
- Каллан Р. Основные концепции нейронных сетей.: Пер. с англ.: Изд. дом «Вильямс», 2001.
- Чипига А.Ф., Воронкин Р.А. Реализация элитного отбора в математической модели мажоритарного генетического алгоритма //Системы управления и информационные технологии №2(19). - Москва-Воронеж, Научная книга, 2005.