Актуальность измерений энергии, затрачиваемой на вращательное движение протяженного твердого тела в среде (жидкости, воздухе), не подлежит обсуждению. В большинстве случаев прямые измерения мощности, потребляемой тем или иным двигателем, не являются достаточными из-за их неоднозначности и низкой точности. Теоретические расчеты, так или иначе, связаны с необходимостью определения других параметров, таких как коэффициент аэродинамического сопротивления, что сводит практическую значимость результатов расчета к нулю [1]. С другой стороны, из закона сохранения энергии следует, что если в момент времени ti угловая скорость тела, на которое действуют только силы диссипации, равнялась wi, а в момент времени ti+1 соответствующее значение угловой скорости - wi+1, то мощность, затрачиваемая телом, момент инерции которого - J, есть ничто иное, как
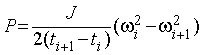 .
.
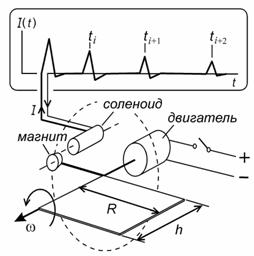
Рис. 1. Схема эксперимента
Проблема, следовательно, заключается в точном измерении угловой скорости как функции времени. Зависимость
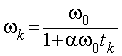
с неопределенными параметрами a и w0 предполагает только одно: квадратичный характер зависимости неконсервативных сил от скорости тела. Поскольку угловая скорость w связана с углом поворота j соотношением w=dj/dt, то неизвестные параметры a и w0 являются нетривиальным аналитическим решением системы уравнений
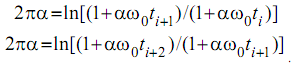
Следовательно
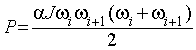 .
.
Выводы настоящей работы достаточно неординарны, должны допускать независимую проверку, поэтому методика проведения измерений и обработки результатов описана подробно. Например, для экспериментальной установки (рис. 1), в которой исследуемым телом является плоскость с размерами h=0.048м, R=0.1м, зависимость мощности P от угловой скорости вращения w0 показана на рис. 2. Оказалось, что теряемая при вращении энергия достаточно хорошо описывается выражением
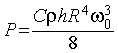
с коэффициентом сопротивления C, равным 1.1 [2] (сплошная кривая на рис. 2; ρ - плотность среды). При этом обязательно надо упомянуть, что для вращающейся плоскости коэффициент аэродинамического сопротивления, по крайней мере, вдвое больше, чем в статическом режиме [3]. Ни к какому нарушению закона сохранения энергии это, однако, не приводит. Потери энергии в основном создаются периферийной областью вращающейся плоскости. В величину силы аэродинамического сопротивления существенный вклад вносит область, близкая к оси вращения, где линейная скорость минимальна. Это основной вывод настоящей работы. Без него пришлось бы смириться с завышенным значением мощности двигателя, необходимой для подержания вращения с постоянной угловой скоростью. При этом реальность создания летательного аппарата с вращающимися плоскими крыльями [4] оказалась бы под угрозой.
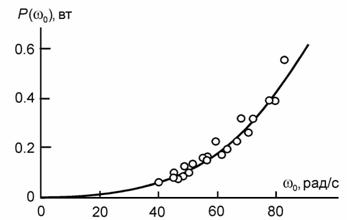
Рис. 2. Потери энергии как функция частоты
СПИСОК ЛИТЕРАТУРЫ:
- Герасимов С.А. Эпициклоидное и поперечное вращение плоского крыла. // Фундаментальные исследования. 2007. № 5. С. 16-19.
- Sovran G., Morel T., Mason W.T. Aerodynamic Drag Mechanisms of Bluff Bodies and Road Vehicles. - New York: Plenum Press, 1978. - 360 p.
- Благодарный В.В. Маятник Максвелла в опытах по аэродинамике. // Учебная физика. 2007. № 1. С. 103-106.
- Герасимов С.А. Летательный аппарат с полупериодным экранированием вращающегося крыла. // Техника и технология. 2007. № 1. С. 8-10.



