При передаче дискретных сигналов по каналу связи вследствие амплитудных и фазовых искажений может возникать межсимвольная интерференция (МСИ), которая ведет к разрушению структуры сигнала, что неизбежно приводит к ухудшению качества приема. В такой ситуации повышение мощности сигнала без дополнительной обработки не всегда улучшает достоверность приема. Разработка новых методов борьбы с МСИ, направленных на повышение помехоустойчивости приема, является актуальной задачей.
Одним из эффективных методов борьбы с МСИ является применение адаптивных выравнивателей (АВ). АВ представляет собой цифровой фильтр с перестраиваемыми весовыми коэффициентами (ВК), который добавляется перед демодулятором. Перестройка ВК осуществляется в соответствии с алгоритмами выравнивания, которые можно разделить на две группы: выравнивание с применением обучающей последовательности и выравнивание вслепую.
В первом случае в начале сеанса связи передается дополнительная обучающая последовательность, которая также известна на приемной стороне и используется как эталонная. В процессе приема сигнала возможны случайные сбои, вследствие чего необходима повторная передача обучающей последовательности.
Во втором случае настройка ВК происходит в результате анализа сигнала на выходе АВ на соответствие определенному критерию. Одним из наиболее известных и эффективных критериев выравнивания вслепую является критерий (функция стоимости) Годара.
Функция стоимости Годара может быть записана в виде [1]:
, (1)
где yk - k-ый отсчет сигнала на выходе АВ; р>0 - целое число; Rp - положительная константа.
При этом алгоритм выравнивания выглядит следующим образом [1]:
, (2)
где Ck - текущий вектор ВК АВ; Ck+1 - вычисляемый вектор ВК АВ; Δ - шаг подстройки; 
- вектор входных комплексно-сопряженных отсчетов.
Алгоритм Годара (2) показывает хорошие результаты при обработке сигналов с постоянной огибающей.
Также стоит отметить, что помехоустойчивость приема во многом зависит от выбора сигнальных форматов. Модулированные сигналы с непрерывной фазой (МНФ) представляются перспективными к использованию в системах передачи цифровой (дискретной) информации вследствие хороших спектральных и энергетических характеристик.
Математически сигналы семейства МНФ описываются следующей формулой [2]:
, (3)
где E - энергия сигнала на одном тактовом интервале, Т - длина тактового интервала, ω0 - несущая частота сигнала, φ0 - начальная фаза сигнала.
Функция φ(t,Ci) описывает поведение фазы сигнала МНФ:
, (4)
где hk - индекс модуляции на k-ом тактовом интервале, q(t) - функция фазового импульса (ФИ), Ci = [c1, c2, .....,ci] - последовательность m-ичных информационных символов.
Сигнал МНФ с индексом модуляции hk = 0,5 и фазовым импульсом 
имеет собственное название - манипуляция минимальным сдвигом (ММС) и широко применяется в современных системах связи.
На основе алгоритма Годара (2) разработан новый алгоритм выравнивания, в котором дополнительно учитывается фазовая структура ММС-сигнала. Алгоритм основан на нескольких функциях стоимости, которые могут быть записаны в виде:
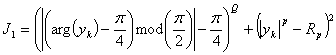, (5)
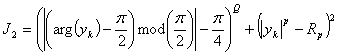, (6)
где Q = 2,4,...; Rp - константа (Rp > 0); p = 2,4,...; yk - очередной отсчет на выходе АВ.
На основании функций стоимости (5) подстройка вектора ВК осуществляется по формуле:
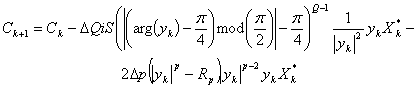, (7)
где S = 1 при 
; S = -1 при 
; i - комплексное число: Re(i)=0; Im(i)=1.
На основании функции стоимости (6) подстройка вектора ВК осуществляется по формуле:
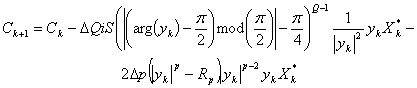. (8)
Для предлагаемого алгоритма определен следующий порядок обработки отсчетов входного ММС-сигнала:
- На границах соседних информационных символов применяется формула (7).
- В середине информационных символов применяется формула (8).
- Для остальных отсчетов применяется формула (2).
Применение предложенного алгоритма показало при компьютерном моделировании повышение помехоустойчивости приема ММС-сигнала в условиях двулучевого распространения на 1,7 дБ при вероятности ошибочной демодуляции информационного символа 1*10-5 по сравнению с известным алгоритмом Годара.
СПИСОК ЛИТЕРАТУРЫ:
- Dominique N. Godard Self-recovering equalization and carrier tracking in two-dimensional data communication systems // IEEE Transactions on communications, Vol. COM-28, №11, Nov. 1980. - PP. 1867-1875.
- Емельянов П.Б., Парамонов А.А. Дискретные сигналы с непрерывной фазой // Зарубежная радиоэлектроника. - 1990. - №12. -
с.17-34.