Составление расписания учебных занятий в вузе является одной из самых сложных задач автоматизации учебного процесса. Кредитная технология обучения с индивидуальной траекторией обучения студента и наличием как постоянных, так и временных учебных групп значительно повышает степень сложности этой задачи. Исходные данные являются неупорядоченным множеством элементов, которые представляют три распределяемых ресурса: студентов, преподавателей и учебных аудиторий. Формами аудиторных занятий являются лекции, практические, лабораторные занятия, СРСП, которые проводятся на потоках, группах и подгруппах. Одним из основных исходных данных для составления расписания является контингент студентов. Поток студентов представляет собой группы студентов с одинаковой специальностью, курсом и языком обучения. Для решения задачи составления расписания, контингент студентов будет представлять собой потоки студентов, а также будет включать в себя всю информацию, относящуюся к потокам, такую, как номер потока, номер группы, количество подгрупп в группе, количество студентов и т.п. Таким образом, минимальной единицей количества студентов является подгруппа. При линейной системе обучения подгруппа является неизменной величиной для всех видов занятий. При этом на потоке, состоящем в общем случае из нескольких групп, занятия проводятся по одному рабочему учебному плану, что позволяет формировать расписание занятий в виде сетки, в столбцах которой расположены погруппы/группы/потоки, а в строках - таймслоты. Максимальной единицей количества студентов при этом является поток.
Кредитная технология обучения позволяет каждому студенту обучаться с индивидуальным выбором порядка изучения дисциплин, что приводит к тому, что максимальной единицей количества студентов
является не поток, а специальность (при обучении на двух языках, например казахском и русском, получим специальности казахского и русского отделения). Минимальной единицей количества студентов также является подгруппа, но эти подгруппы/группы/ потоки будут в общем случае различны для всех изучаемых дисциплин. Если рассматривать кредитную технологию обучения только с учетом курсов по выбору без возможности изменения порядка изучения учебных дисциплин, то получим как постоянные, так и временные потоки/группы/подгруппы.
Автоматизация составления расписания учебных занятий является одной из важнейших задач при управлении учебным процессом вуза. Декомпозиция этой задачи значительно ускоряет процесс получения решения. Если в вузе предусмотрены занятия по военной подготовке, то для каждого факультета устанавливается произвольно, или с использованием соответствующего алгоритма оптимизации один или два учебных дня для их проведения.
После выбора учебного дня для проведения занятий по военной подготовке нетрудно определить учебные поручения, которые можно поставить в расписание в указанный день. Так как учебные поручения были предварительно отсортированы по степени загруженности преподавателей и аудиторий, а также сформированы группы аудиторий, в которых могут проводиться занятия, то список учебных поручений на выбранный день для каждого факультета также будет отсортирован. Задачей составления расписания на этот день недели является наилучшее использование закрепленного за факультетом аудиторного фонда.
В общем случае имеется объем учебных поручений, превышающий имеющийся аудиторный фонд. Составить расписание учебных занятий - это значит выбрать из всего объема компонентов дисциплин наиболее подходящие и расположить их по таймс-лотам оптимальным в смысле выбранного критерия образом. Для каждой части потоков, представленных в избыточном списке учебных поручений и имеющих временные группы, введем кроме основных объектов - группы/преподаватели/аудитории, вспомогательные объекты - связки компонентов дисциплин. Вспомогательные объекты предназначены для сокращения перебора при составлении расписания. Эти объекты следует формировать таким образом, чтобы получить суммарное количество студентов, соответствующее постоянной подгруппе/группе/ потоку.
Для генерации расписания применяется эвристический алгоритм, который ищет назначение очередного учебного поручения и варианты переназначения ранее спланированных занятий, конфликтующих с очередным. Формой оценки качества расписания является аддитивный критерий оптимальности, учитывающий нормированные значения методических и организационных критериев оптимальности. Весовые коэффициенты целевой функции устанавливаются постоянными.
Обозначим избыточное множество учебных поручений для выбранного учебного дня {dip,k } , где i=1, N;p=1, P; k=1,K. N, Р, К соответственно общее количество учебных поручений, преподавателей и групп аудиторий заданного множества. Для каждого учебного поручения задаем количество часов (не более 2), допустимые таймслоты, преподавателя, группу аудиторий, родительские учебные поручения, которые позволяют построить граф компонентов для каждой дисциплины на потоке, тип групп, а также список подгрупп в которых проводится данное занятие. Кроме этого формируется матрица G групп аудиторий, включающая номер аудитории, ее вместимость и ссылку на вложенную группу. Дополнительно определяется матрица занятости преподавателей, включающая уже поставленные в расписание занятия, а также его пожелания и степень важности их учета. Для каждой основной подгруппы определим количество часов учебных занятий в заданном множестве учебных поручений, которое позволяет определить оптимальное количество часов в расписании этой подгруппы. Для компонентов дисциплин с временными группами определим долю студентов из постоянных подгрупп, что позволяет учесть эту долю в постоянных подгруппах.
Рассмотрим ограничения на выбор учебных поручений в расписание занятий и сформируем целевую функцию. Количество часов по каждой компоненте не превышает двух по условию формирования избыточного списка. Количество часов по каждой дисциплине по всем видам занятий не превышает 4 часов. Для выполнения этого условия следует учесть ссылку на родительскую компоненту. Обозначим R(d) родительскую компоненту для d. Пусть M(g,t) матрица расписания, где g-подгруппа, t-таймслот. Для компонент с временными группами ячейка матрицы может содержать несколько совместимых учебных поручений.
R(R(Mi,j (d))) <> Mi,z(d), z = 
где w - общее количество таймслотов.
Занятия для двухчасовых компонентов проводятся в виде пары.
(Мi,j - Мi,j-1) (Мi,j - Мi,j+1) = 0, если компонента Мi,j двухчасовая.
Введем матрицу занятости подгрупп:
Отсутствие окон у подгрупп определяется следующим образом:
Кроме того, задается ограничение на количество занятий в каждой подгруппе:
В каждом таймслоте общее количество занятых аудиторий в каждой группе аудиторий не превышает их общего количества Sk с учетом вложенности групп аудиторий. Определим количество занятых аудиторий в каждой группе аудиторий в каждом таймслоте. Для этого введем матрицу A(g,t) групп аудиторий расписания занятий. При этом следует учитывать, что для тех элементов матрицы M(g,t), которые содержат список элементов компонентов дисциплин, матрица A(g,t) также содержит список элементов групп аудиторий, но каждый компонент учитывается только один раз.
Обозначим Vk,t - количество аудиторий в k-той группе аудиторий в t- тый таймслот. Для всех групп аудиторий, для которых нет вложенных групп, выполняется условие: Vk,t ≤ Sk , для остальных следующее условие: 
, где q вложенная группа. Суммирование выполняется последовательно для количества вложенных групп от последней до первой. Так, например, если имеется 4 вложенных группы аудиторий 1∈2∈З∈4,то должны выполняться следующие условия:
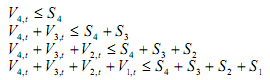
В качестве целевой функции можно использовать выбор наибольшего количества учебных поручений из избыточного для составления расписания:
, где аi = 1, если компонента поставлена в~расписание и равна нулю в противном случае.
Такой подход является допустимым, если все группы аудиторий являются равно загруженными. При наличии групп аудиторий с критичной загруженностью следует использовать целевую функцию в виде: 
, где хi - весовой коэффициент группы аудитории i-того компонента.
Формирование оптимального расписания учебных занятий для одного учебного дня, дня военной подготовки на факультете, позволяет провести декомпозицию общей задачи и значительно уменьшить размерность задачи.