В процессе проектирования и эксплуатации технической системы уделяют внимание вопросам её надежности и живучести. Чтобы обеспечить требуемые качества открытой системы, человек принял на себя роль управления, для реализации которого берется точка отсчета по времени и рассматриваются наиболее вероятные состояния [1]. Частота и продолжительность состояний элементов структуры системы зависит от уровня, числа и мощности факторов воздействия, включая управленческие решения. Например, с позиции анализа структурной надежности состояния могут быть описаны временем отказа и наработки на отказ, частотой возникновения событий [2], относящихся к появлению работоспособного и неработоспособного состояний элементов системы. Эти показатели востребованы со стороны подсистемы управления с целью сохранения/повышения уровня структурной надежности технического объекта. Кроме этого, они применимы и для определения такого показателя как количество информации, присущей каждому из элементов и системе в целом. Рассматривая его дополнительно в качестве критерия структуры системы, можно судить о её состоянии, которое отвечало бы предустановленным требованиям по надежности.
Особенности применения выражения Шеннона в задаче определения количества энтропии
Обратимся далее к вопросу об некоторых особенностях в определении количества информации при анализе состояний технической системы. Теория информации рассматривает возможности применения «информации» с количественной стороны. Тем не менее анализ и моделирование процессов взаимодействия элементов системы через выражение информации с качественной стороны можно также считать целесообразными. В данном случае информация разделяется на составляющие согласно качественным признакам, каждая из которых рассматривается как количественная характеристика интерпретации статистических данных. Разделение по качественному признаку количества информации – результат привязки доли информации к каждому из выделенных свойств системы.
В информатике существует несколько подходов к измерению информации, одним из которых является энтропийный подход, не исключающий возможности его применения к анализу надежности и живучести технических систем [1]. Данный подход позволяет определять (измерять) информационную энтропию, содержащуюся в исследуемом объекте относительно объектов, с которыми он взаимодействует. Здесь доступны методы, большинство из которых предусматривает подход К. Шеннона в определении количества информации для дискретных систем:
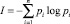
при условии, 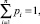 (1)
(1)
где pi – вероятность появления события i = 1, 2, ..., n.
Далее рассмотрим возможности применения (1) в оценке структурной надежности систем. С целью определения уровня надежности системы, состояния элементов (работоспособное и неработоспособное) обусловлены появлением непересекающихся, противоположных и качественно различающихся событий. Для определения количества информации строят статистический ансамбль данных (например, согласно [8]), отражающий на длительном интервале времени процесс вероятностной смены состояний. Фиксированные по времени состояния являются исходными данными определения средней величины вероятностей состояний: работоспособного p и неработоспособного q. Определить количество информации можно по выражению (1). Однако оно не позволяет разделить информацию по качественному признаку. Применение данного выражения будет справедливым лишь для частного случая, когда рассматривается лишь один элемент системы, с предположением о его полной независимости состояний. В этом случае на основе построенного ансамбля статистических данных и предположения о неизменности значений вероятности появления событий в будущем можно определить в соответствии с мерой Шеннона информационную энтропию по выражению
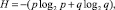
при условии: p + q = 1. (2)
Основание 2 при логарифме свидетельствует о том, что рассматриваются два состояния: работоспособное и неработоспособное/отказ.
Однако существует ряд причин, по которым выражение (2) не может быть использовано для анализа структуры системы в целом. Поясним данное обстоятельство. Поскольку информация должна быть разделена на качественные составляющие, невозможно обойти стороной наличие топологии структуры системы. Сложные системы включают в себя множество элементов, и отказ одного из них приводит к отказам (неработоспособному состоянию) других элементов. Наличие причинно-следственной связи означает то, что элементы зависимы и их взаимосвязанные состояния образуют пересекающиеся события [3, 4]. Следовательно, процедура определения результирующей информации является сложной (как показано в [2]), должна выполняться по разработанным алгоритмам (например, посредством эквивалентных преобразований структуры системы согласно [7]).
Сама сложность заключается не в формуле (2), а в определении результирующих значений вероятностей работоспособного P и неработоспособного Q состояний системы. Например, их вычисление для пересекающихся i-х и j-х состояний можно записать в общей форме:
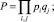
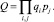 (3)
(3)
Количество выражений вида (3) может быть огромным, равным 2n, где n – число элементов системы, 2 – количество рассматриваемых состояний элемента. Результирующие значения согласно (3) можно определить для каждой из решаемых задач в отдельности, используя методы ветвей и границ, перебора состояний и др. Что касается получения количества информации, то можно рекомендовать метод, представленный в [6].
Качественное значение энтропии
В теории надежности события рассматриваются как случайные, характеризуясь значениями вероятности работоспособного и неработоспособного состояний, оставляя при этом в стороне вопросы неопределенности информации. Для более полного анализа структурного содержания системы, её надежности востребован качественный подход, разделяющий общее количество информационной энтропии на составляющие.
Поскольку между теорией информации и теорией вероятностей существует связь (так как в каждой из них рассматриваются состояния и события), то, принимая во внимание (3), можно определить количество информационной (суммарной) энтропии о состоянии системы за рассматриваемый период:
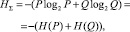 (4)
(4)
при условии: P + Q = 1. Здесь H(P), H(Q) – информационные энтропии, соответственно работоспособного и неработоспособного состояний системы.
Рассмотрим особенности понятийного характера упомянутых состояний, относящихся к содержанию слова «энтропия». Что касается H(Q), то вопрос о правомочности её определения не стоит так остро, как с H(P). Дело в том, что энтропия неработоспособного состояния непосредственно обусловлена наличием вероятностных признаков появления непредвиденных событий. Тем самым она отражает природу неопределенности информации, что нельзя сказать об энтропии работоспособного состояния. Если рассматривать H(P) с точки зрения наличия в системе определенной информации, то (при многообразии её определений) она характеризует наличие совокупности сведений о состояния системы, когда её элементы выполняют заданные функции. При этом не исключен вероятностный характер отражения работоспособного состояния, что позволяет связать H(P) со словом «энтропия». В дополнение к изложенному высказыванию отметим: не исключаются из рассмотрения такие определения, как «информация» и «энтропия», с целью разделения по качественному признаку соответственно величин H(P) и H(Q).
Далее представим пояснения, относящиеся к важности учета качественной составляющей в определении энтропии. От искусственной системы требуется повышенный уровень надежности, и, следовательно, она должна обладать большей информативностью и меньшей неопределенностью. Здесь можно выделить два предельных случая энтропии неработоспособного состояния:
1) практически нулевая энтропия [3], свидетельствующая о наличии максимальной энтропии работоспособного состояния;
2 высокая энтропия, характеризующая критическое содержание работоспособного состояния системы. В первом случае мы с высокой долей вероятности полагаем, что система в будущем будет обладать высоким уровнем надежности, тогда как во втором – предельным, с точки зрения возможностей существования (необходимости дальнейшей эксплуатации) технической системы.
Взаимная связь между этими случаями и предположение о независимости возникновения противоположных событий свидетельствуют о значимости процесса разделения количества энтропии на качественные составляющие согласно (4). Выражение (4) можно обобщить и на случай представления энтропии через её нормировку [5]:
H*(P) + H*(Q) = n, (5)
где n – количество элементов в системе, а «звездочка» означает наличие нормированного значения энтропии.
В процессе анализа энтропийного содержания системы H(P) можно рассматривать как ресурсы, обеспечивающие её надежное функционирование, а H(Q) – как ресурсы, выбывшие (изъятые) из системы под воздействием внешних сил (сил Природы).
Смысл соотношения энтропий в (4) заключается в следующем. Техническая система, являясь открытой, находится в некоторой среде, при движении в которой структура видоизменяется, а заложенные в неё ресурсы выбывают под воздействием сил Природы. По причине отсутствия достоверных знаний о движении среды эти диссипативные процессы (с некоторой долей вероятности) предлагается учесть через H(Q). В реальности (с позиции анализа структурной надежности) величина H(Q) невелика по сравнению HΣ. Однако, если судить об объемах прекращения подачи энергоресурсов в отдельные узлы системы, то такое утверждение будет неправомерным, поскольку речь уже идет о функциональной надежности. С целью сохранения системы от дальнейшего разрушения требуют вовлечения дополнительных ресурсов, что и приведет к снижению неопределенности, выраженной через увеличение H(P). Следовательно, эти две составляющие энтропии находятся в соотношении между собой. Между ними происходит взаимообмен: с одной стороны, значение H(Q) предопределяет величину H(P), поскольку отражает видоизменение структуры под влиянием внешних воздействий, с другой – H(P) видоизменяет структуру и H(Q), вследствие целенаправленного вмешательства человека в систему, снимая тем самым неопределенность.
Разграничение по уровню состояний системы
Энтропию можно использовать в качестве величины, характеризующей уровень структурной надежности системы, поскольку её характеристики наделены свойствами:
? определения меры неопределенности (в структуре и поведении) состояний системы в количественном виде, выражаясь через её вероятностные характеристики;
? зависимости от размерности пространства состояний системы, числа её элементов и топологии структуры;
? отсутствия необходимости выбора начала координат в пространстве состояний системы;
? разделения полученной информации о состояниях системы по качественному признаку.
Опираясь на данные свойства и выражения (4), измерить качественные соотношения энтропии можно через относительную величину:
G(P) = H(P)/HΣ;
G(Q) = H(Q)/HΣ; G(P) + G(Q) = 1. (6)
Аналогично, применяя (6), относительные величины:
G(P) = H*(P)/n;
G(Q) = H*(Q)/n; G(P) + G(Q) = 1. (7)
Таким образом, приведенный показатель G разграничивает качественно различающиеся состояния системы, проводя тем самым уровень/границу в рамках суммарной энтропии всей системы.
Определение показателя, по сути свидетельствующего об уровне структурной надежности, должно производиться в следующем порядке:
? на основе составленной структуры выбирается способ определения значений энтропии H(P) и H(Q);
? вычисляются значения H(P) и H(Q) анализируемой системы;
? вычисляется HΣ;
? определяются значения G(P) и G(Q), или G(Q) = 1 – G(P).
Применение показателя G – возможность оценки уровня структурной надежности посредством разграничения (проведение границы) между работоспособным и неработоспособным состояниями технической системы.
Выделим свойства показателя G:
? при соотношении G(Q)/G(P) = 0 – система обладает идеальной структурной надежностью, а при G(P)/G(Q) = 0 – структура отсутствует;
? рост G(P) свидетельствует о развитии системы, а рост G(Q) – о её деградации;
? дополнительное внесение в структуру резервирующих элементов (расширение системы) отмечается ростом G(P).
Справедливость данных свойств подтверждена применением метода, предложенного в работе [6].
Заключение
Одним из важных вопросов в области оценки надежности технической системы можно считать меру количества присущей ей информации. Рассматривая структурную надежность, важно разделить состояния её структурных элементов на две качественно противоположные составляющие: работоспособное состояние и неработоспособное. Каждому из этих противоположных состояний присуща своя энтропия. Определив отдельно по каждому качественному признаку энтропию, можно вычислить показатель разграничения уровня структурной надежности. Сопоставляя между собой показатели, можно оценить долю присутствия энтропии неработоспособного состояния в общем объеме полученной информации, присущей всей структуре системы. Такой показатель весьма полезен в качестве критерия при решении задач оптимизации структур систем.
Данный показатель отражает наличие топологии структуры, разнообразие и зависимость множества противоположных состояний между собой. Тем самым в качестве показателя уровня структурной надежности допустимо использование отношения энтропии неработоспособного состояния системы H(Q) и суммарной энтропии HΣ при наложенных на систему ограничениях. Такой показатель позволяет судить о состоянии системы и её структурной надежности: значения показателя убывают при расширении (эволюции) системы, если относительное приращение суммарной энтропии системы не меньше относительного приращения энтропии неработоспособного состояния.
Работа выполнена при финансовой поддержке РФФИ в рамках научного проекта № 15-08-01473а.
[1] Состояние рассматривается как устойчивое свойство объекта на выбранном интервале времени, до момента, когда возникший фактор переведет его в противоположное состояние.
[2] Событие рассматривается как результат перехода объекта из одного состояния в другое – противоположное.
[3] В природе нулевой энтропии не существует.
Библиографическая ссылка
Дулесов А.С., Дулесова Н.В., Карандеев Д.Ю. ПОКАЗАТЕЛЬ РАЗГРАНИЧЕНИЯ УРОВНЯ НАДЕЖНОСТИ ТЕХНИЧЕСКОЙ СИСТЕМЫ ПО КАЧЕСТВЕННОМУ ПРИЗНАКУ: ЭНТРОПИЙНЫЙ ПОДХОД // Фундаментальные исследования. 2016. № 2-3. С. 477-481;URL: https://fundamental-research.ru/ru/article/view?id=39959 (дата обращения: 01.04.2025).



